MIMO Model Identification

Multiple Input, Multiple Output (MIMO) systems can be empirically described by several linear dynamic system models. MIMO systems are more complicated than Single Input, Single Output (SISO) systems because of several factors including multivariate interaction, potential co-linearity of inputs, and large data processing requirements. Some common MIMO model forms include:

Model identification in these forms typically involves fitting unknown coefficients in the model followed by an analysis to determine how many parameters are statistically significant.

Exercise

The following data set was generated in class from two voltage inputs (u) that changed the temperature (x) of two thermistors from the Arduino Lab.

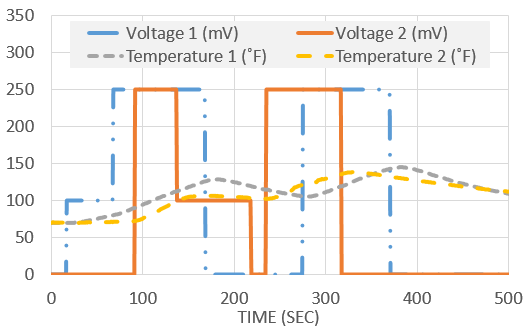
Download Dynamic Model Identification Files (Excel, MATLAB, Python)
Download Dynamic Data

Determine a linear dynamic model that best describes the input to output relationship between voltage and temperature. Compute the steady state gain for each input to output relationship. Data and example script files are posted above in Excel and MATLAB.

Solution (Excel, MATLAB, Python)

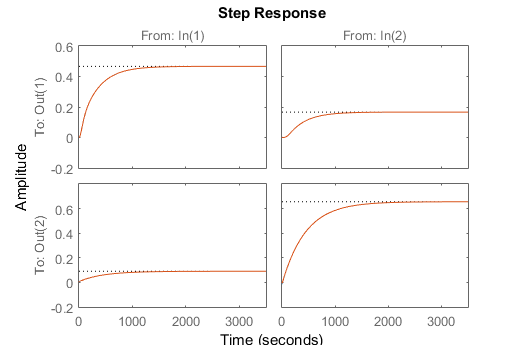
Solution to Dynamic Model Identification (Excel and MATLAB)
Solution to Dynamic Model Identification Files (Python)

Solution (GEKKO Python)

from gekko import GEKKO
import pandas as pd
import matplotlib.pyplot as plt

# load data and parse into columns
url = 'http://apmonitor.com/do/uploads/Main/tclab_dyn_data2.txt'
data = pd.read_csv(url)
t = data['Time']
u = data[['H1','H2']]
y = data[['T1','T2']]

# generate time-series model
m = GEKKO(remote=False)

# system identification
na = 2 # output coefficients
nb = 2 # input coefficients
yp,p,K = m.sysid(t,u,y,na,nb,diaglevel=1)

plt.figure()
plt.subplot(2,1,1)
plt.plot(t,u)
plt.legend([r'$u_0$',r'$u_1$'])
plt.ylabel('MVs')
plt.subplot(2,1,2)
plt.plot(t,y)
plt.plot(t,yp)
plt.legend([r'$y_0$',r'$y_1$',r'$z_0$',r'$z_1$'])
plt.ylabel('CVs')
plt.xlabel('Time')
plt.savefig('sysid.png')
plt.show()
[$[Get Code]]

from gekko import GEKKO
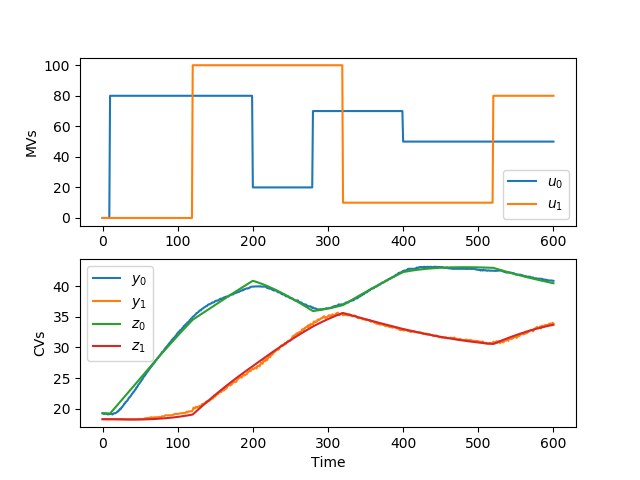
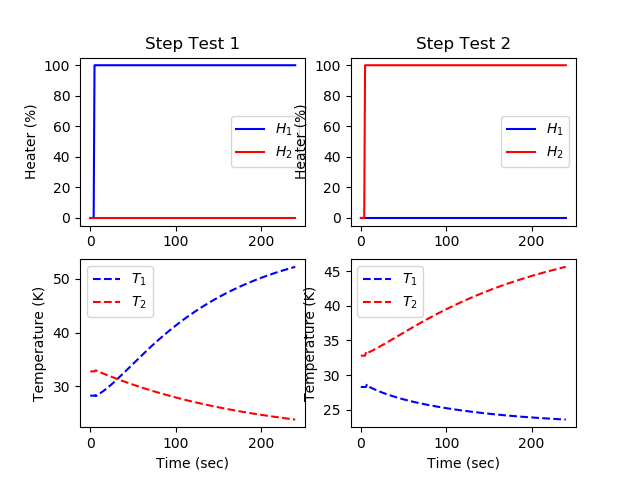
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# load data and parse into columns
url = 'http://apmonitor.com/do/uploads/Main/tclab_dyn_data2.txt'
data = pd.read_csv(url)
t = data['Time']
u = data[['H1','H2']]
y = data[['T1','T2']]

# generate time-series model
m = GEKKO(remote=False)

# system identification
na = 3 # output coefficients
nb = 4 # input coefficients
yp,p,K = m.sysid(t,u,y,na,nb)

plt.figure()
plt.subplot(2,1,1)
plt.plot(t,u)
plt.legend([r'$H_1$',r'$H_2$'])
plt.ylabel('MVs')
plt.subplot(2,1,2)
plt.plot(t,y)
plt.plot(t,yp)
plt.legend([r'$T_{1meas}$',r'$T_{2meas}$',\
            r'$T_{1pred}$',r'$T_{2pred}$'])
plt.ylabel('CVs')
plt.xlabel('Time')
plt.savefig('sysid.png')

# step test model
yc,uc = m.arx(p)

# steady state initialization
m.options.IMODE = 1
m.solve(disp=False)

# dynamic simulation (step tests)
m.time = np.linspace(0,240,241)
m.options.TIME_SHIFT=0
m.options.IMODE = 4
m.solve(disp=False)

plt.figure()

# step for first MV (Heater 1)
uc[0].value = np.zeros(len(m.time))
uc[0].value[5:] = 100
uc[1].value = np.zeros(len(m.time))
m.solve(disp=False)

plt.subplot(2,2,1)
plt.title('Step Test 1')
plt.plot(m.time,uc[0].value,'b-',label=r'$H_1$')
plt.plot(m.time,uc[1].value,'r-',label=r'$H_2$')
plt.ylabel('Heater (%)')
plt.legend()
plt.subplot(2,2,3)
plt.plot(m.time,yc[0].value,'b--',label=r'$T_1$')
plt.plot(m.time,yc[1].value,'r--',label=r'$T_2$')
plt.ylabel('Temperature (K)')
plt.xlabel('Time (sec)')
plt.legend()

# step for second MV (Heater 2)
uc[0].value = np.zeros(len(m.time))
uc[1].value = np.zeros(len(m.time))
uc[1].value[5:] = 100
m.solve(disp=False)
plt.subplot(2,2,2)
plt.title('Step Test 2')
plt.plot(m.time,uc[0].value,'b-',label=r'$H_1$')
plt.plot(m.time,uc[1].value,'r-',label=r'$H_2$')
plt.ylabel('Heater (%)')
plt.legend()
plt.subplot(2,2,4)
plt.plot(m.time,yc[0].value,'b--',label=r'$T_1$')
plt.plot(m.time,yc[1].value,'r--',label=r'$T_2$')
plt.ylabel('Temperature (K)')
plt.xlabel('Time (sec)')
plt.legend()

plt.show()
[$[Get Code]]

References

Home | MIMO Model Identification