Model Predictive Control, or MPC, is an advanced method of process control that has been in use in the process industries such as chemical plants and oil refineries since the 1980s. Model predictive controllers rely on dynamic models of the process, most often linear empirical models obtained by system identification. APMonitor and GEKKO support continuous or discrete state space and autoregressive exogenous (ARX) input models.
Discrete State Space in GEKKO
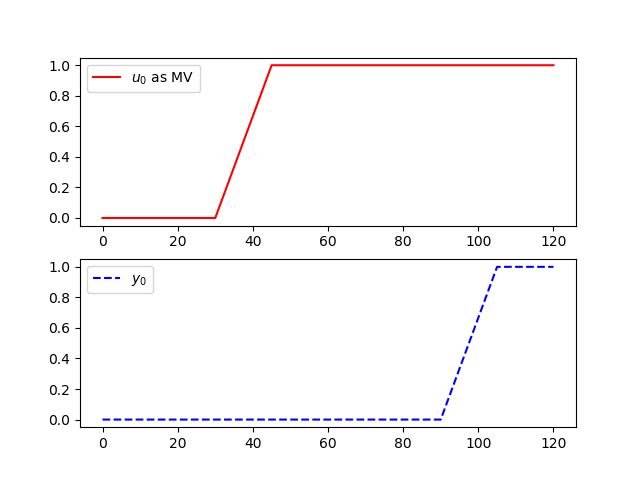
The following is an example of implementing a discrete state space model for an input delay of 60 seconds. The sample time for this model is 15 seconds.
import numpy as np
from gekko import GEKKO
A = np.array([[0,0,0,0],
[1,0,0,0],
[0,1,0,0],
[0,0,1,0]])
B = np.array([[1],
[0],
[0],
[0]])
C = np.array([[0, 0, 0, 1]])
#%% Build GEKKO State Space model
m = GEKKO()
x,y,u = m.state_space(A,B,C,D=None,discrete=True)
# customize names
mv0 = u[0]
# CVs
cv0 = y[0]
m.time = np.linspace(0,120,9)
mv0.value = np.zeros(9)
mv0.value[3:9] = 1
m.options.imode = 4
m.options.nodes = 2
m.solve() # (GUI=True)
# also create a Python plot
import matplotlib.pyplot as plt
plt.subplot(2,1,1)
plt.plot(m.time,mv0.value,'r-',label=r'$u_0$ as MV')
plt.legend()
plt.subplot(2,1,2)
plt.plot(m.time,cv0.value,'b--',label=r'$y_0$')
plt.legend()
plt.show()
from gekko import GEKKO
A = np.array([[0,0,0,0],
[1,0,0,0],
[0,1,0,0],
[0,0,1,0]])
B = np.array([[1],
[0],
[0],
[0]])
C = np.array([[0, 0, 0, 1]])
#%% Build GEKKO State Space model
m = GEKKO()
x,y,u = m.state_space(A,B,C,D=None,discrete=True)
# customize names
mv0 = u[0]
# CVs
cv0 = y[0]
m.time = np.linspace(0,120,9)
mv0.value = np.zeros(9)
mv0.value[3:9] = 1
m.options.imode = 4
m.options.nodes = 2
m.solve() # (GUI=True)
# also create a Python plot
import matplotlib.pyplot as plt
plt.subplot(2,1,1)
plt.plot(m.time,mv0.value,'r-',label=r'$u_0$ as MV')
plt.legend()
plt.subplot(2,1,2)
plt.plot(m.time,cv0.value,'b--',label=r'$y_0$')
plt.legend()
plt.show()
The discrete state space with 4 steps of delay is also possible with a time series (ARX) model using the Gekko delay function.
Also see