TCLab A - SISO Digital Twin
Main.TCLabA History
Hide minor edits - Show changes to markup
background-color: #0000ff;
background-color: #1e90ff;
width: 300px;
width: 100%;
- Virtual Lab A on Google Colab
Virtual TCLab on Google Colab
(:toggle hide gekko_labAf button show="Lab A: Python GEKKO SISO ARX":) (:div id=gekko_labAf:)
(:toggle hide gekko_labA_ARX button show="Lab A: Python GEKKO SISO ARX":) (:div id=gekko_labA_ARX:)
(:toggle hide gekko_labAe button show="Lab A: Python GEKKO SISO ARX":)
(:toggle hide gekko_labAf button show="Lab A: Python GEKKO SISO ARX":)
plt.show() (:sourceend:) (:divend:)
(:toggle hide gekko_labAe button show="Lab A: Python GEKKO SISO ARX":) (:div id=gekko_labAf:)
- see https://apmonitor.com/wiki/index.php/Apps/ARXTimeSeries
from gekko import GEKKO import numpy as np import pandas as pd import matplotlib.pyplot as plt
- load data and parse into columns
url = 'http://apmonitor.com/do/uploads/Main/tclab_dyn_data2.txt' data = pd.read_csv(url) t = data['Time'] u = data['H1'] y = data['T1']
m = GEKKO()
- system identification
na = 2 # output coefficients nb = 2 # input coefficients yp,p,K = m.sysid(t,u,y,na,nb,pred='meas')
plt.figure() plt.subplot(2,1,1) plt.plot(t,u,label=r'$Heater_1$') plt.legend() plt.ylabel('Heater') plt.subplot(2,1,2) plt.plot(t,y) plt.plot(t,yp) plt.legend([r'$T_{meas}$',r'$T_{pred}$']) plt.ylabel('Temperature (°C)') plt.xlabel('Time (sec)')
(:title TCLab A - SISO Modeling:)
(:title TCLab A - SISO Digital Twin:)
GEKKO Documentation
TCLab Documentation
(:title TCLab A - Modeling:)
(:title TCLab A - SISO Modeling:)
- Advanced Control Lab Overview
Advanced Control Lab Overview
- TCLab Files on GitHub
- Basic (PID) Control Lab
TCLab Files on GitHub Basic (PID) Control Lab
Lab A
(:title TCLab A - Modeling:) (:keywords Arduino, PID, temperature, control, process control, course:) (:description Energy Balance and Deep Learning with Arduino Data from TCLab:)
The TCLab is a hands-on application of machine learning and advanced temperature control with two heaters and two temperature sensors. The labs reinforce principles of model development, estimation, and advanced control methods. This is the first exercise to simulate an energy balance and compare the predictions to deep learning with a multi-layered neural network.
Lab Problem Statement
Data and Solutions
Lab A
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/SomZYxmIDE8" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> (:htmlend:)
- SISO Energy Balance Solution with MATLAB and Python
- Steady state data, 1 heater
- Dynamic data, 1 heater
(:toggle hide gekko_labAd button show="Lab A: Python TCLab Generate Step Data":) (:div id=gekko_labAd:) (:source lang=python:) import numpy as np import pandas as pd import tclab import time import matplotlib.pyplot as plt
- generate step test data on Arduino
filename = 'tclab_dyn_data1.csv'
- heater steps
Qd = np.zeros(601) Qd[10:200] = 80 Qd[200:400] = 20 Qd[400:] = 50
- Connect to Arduino
a = tclab.TCLab() fid = open(filename,'w') fid.write('Time,H1,T1\n') fid.close()
- run step test (10 min)
for i in range(601):
# set heater value
a.Q1(Qd[i])
print('Time: ' + str(i) + ' H1: ' + str(Qd[i]) + ' T1: ' + str(a.T1))
# wait 1 second
time.sleep(1)
# write results to file
fid = open(filename,'a')
fid.write(str(i)+',str(Qd[i]),str(a.T1)\n')
fid.close()
- close connection to Arduino
a.close()
- read data file
data = pd.read_csv(filename)
- plot measurements
plt.figure() plt.subplot(2,1,1) plt.plot(data['Time'],data['H1'],'b-',label='Heater 1') plt.ylabel('Heater (%)') plt.legend(loc='best') plt.subplot(2,1,2) plt.plot(data['Time'],data['T1'],'r.',label='Temperature 1') plt.ylabel('Temperature (degC)') plt.legend(loc='best') plt.xlabel('Time (sec)') plt.savefig('tclab_dyn_meas1.png')
plt.show() (:sourceend:) (:divend:)
(:toggle hide gekko_labAf button show="Lab A: Python GEKKO Energy Balance":) (:div id=gekko_labAf:)
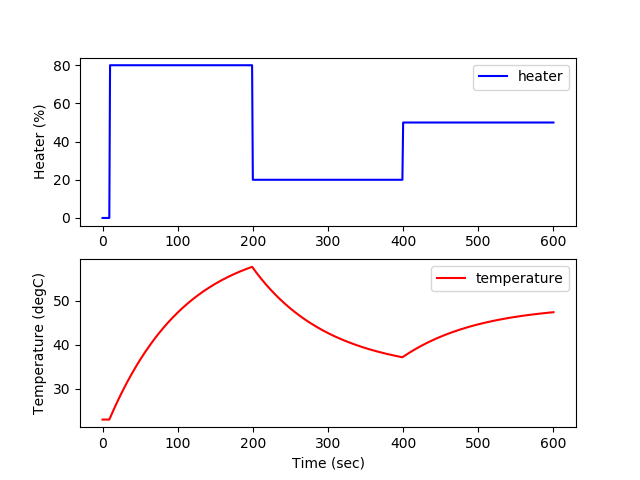
(:source lang=python:) import numpy as np import matplotlib.pyplot as plt from gekko import GEKKO
- initialize GEKKO model
m = GEKKO()
- model discretized time
n = 60*10+1 # Number of second time points (10min) m.time = np.linspace(0,n-1,n) # Time vector
- Parameters
Qd = np.zeros(601) Qd[10:200] = 80 Qd[200:400] = 20 Qd[400:] = 50 Q = m.Param(value=Qd) # Percent Heater (0-100%)
T0 = m.Param(value=23.0+273.15) # Initial temperature Ta = m.Param(value=23.0+273.15) # K U = m.Param(value=10.0) # W/m^2-K mass = m.Param(value=4.0/1000.0) # kg Cp = m.Param(value=0.5*1000.0) # J/kg-K A = m.Param(value=12.0/100.0**2) # Area in m^2 alpha = m.Param(value=0.01) # W / % heater eps = m.Param(value=0.9) # Emissivity sigma = m.Const(5.67e-8) # Stefan-Boltzman
T = m.Var(value=T0) #Temperature state as GEKKO variable
m.Equation(T.dt() == (1.0/(mass*Cp))*(U*A*(Ta-T) + eps * sigma * A * (Ta**4 - T**4) + alpha*Q))
- simulation mode
m.options.IMODE = 4
- simulation model
m.solve()
- plot results
plt.figure(1) plt.subplot(2,1,1) plt.plot(m.time,Q.value,'b-',label='heater') plt.ylabel('Heater (%)') plt.legend(loc='best') plt.subplot(2,1,2) plt.plot(m.time,np.array(T.value)-273.15,'r-',label='temperature') plt.ylabel('Temperature (degC)') plt.legend(loc='best') plt.xlabel('Time (sec)') plt.savefig('tclab_eb_pred.png') plt.show() (:sourceend:) (:divend:)
(:toggle hide gekko_labAe button show="Lab A: Python GEKKO Neural Network":) (:div id=gekko_labAe:)
(:source lang=python:) import numpy as np import pandas as pd import matplotlib.pyplot as plt from gekko import GEKKO import time
- -------------------------------------
- import or generate data
- -------------------------------------
filename = 'tclab_ss_data1.csv' try:
try:
data = pd.read_csv(filename)
except:
url = 'https://apmonitor.com/do/uploads/Main/tclab_ss_data1.txt'
data = pd.read_csv(url)
except:
# generate training data if data file not available
import tclab
# Connect to Arduino
a = tclab.TCLab()
fid = open(filename,'w')
fid.write('Heater,Temperature\n')
# test takes 2 hours = 40 pts * 3 minutes each
npts = 40
Q = np.sin(np.linspace(0,np.pi,npts))*100
for i in range(npts):
# set heater value
a.Q1(Q[i])
print('Heater 1: ' + str(Q[i]) + ' %')
# wait 3 minutes
time.sleep(3*60)
# record temperature and heater value
print('Temperature 1: ' + str(a.T1) + ' degC')
fid.write(str(Q[i])+',str(a.T1)\n')
# close file
fid.close()
# close connection to Arduino
a.close()
# read data file
data = pd.read_csv(filename)
- -------------------------------------
- scale data
- -------------------------------------
x = data['Heater'].values y = data['Temperature'].values
- minimum of x,y
x_min = min(x) y_min = min(y)
- range of x,y
x_range = max(x)-min(x) y_range = max(y)-min(y)
- scaled data
xs = (x - x_min)/x_range ys = (y - y_min)/y_range
- -------------------------------------
- build neural network
- -------------------------------------
nin = 1 # inputs n1 = 1 # hidden layer 1 (linear) n2 = 1 # hidden layer 2 (nonlinear) n3 = 1 # hidden layer 3 (linear) nout = 1 # outputs
- Initialize gekko models
train = GEKKO() test = GEKKO() dyn = GEKKO() model = [train,test,dyn]
for m in model:
# input(s)
m.inpt = m.Param()
# layer 1
m.w1 = m.Array(m.FV, (nin,n1))
m.l1 = [m.Intermediate(m.w1[0,i]*m.inpt) for i in range(n1)]
# layer 2
m.w2 = m.Array(m.FV, (n1,n2))
m.l2 = [m.Intermediate(sum([m.tanh(m.w2[j,i]*m.l1[j]) for j in range(n1)])) for i in range(n2)]
# layer 3
m.w3 = m.Array(m.FV, (n2,n3))
m.l3 = [m.Intermediate(sum([m.w3[j,i]*m.l2[j] for j in range(n2)])) for i in range(n3)]
# output(s)
m.outpt = m.CV()
m.Equation(m.outpt==sum([m.l3[i] for i in range(n3)]))
# flatten matrices
m.w1 = m.w1.flatten()
m.w2 = m.w2.flatten()
m.w3 = m.w3.flatten()
- -------------------------------------
- fit parameter weights
- -------------------------------------
m = train m.inpt.value=xs m.outpt.value=ys m.outpt.FSTATUS = 1 for i in range(len(m.w1)):
m.w1[i].FSTATUS=1
m.w1[i].STATUS=1
m.w1[i].MEAS=1.0
for i in range(len(m.w2)):
m.w2[i].STATUS=1
m.w2[i].FSTATUS=1
m.w2[i].MEAS=0.5
for i in range(len(m.w3)):
m.w3[i].FSTATUS=1
m.w3[i].STATUS=1
m.w3[i].MEAS=1.0
m.options.IMODE = 2 m.options.SOLVER = 3 m.options.EV_TYPE = 2 m.solve(disp=False)
- -------------------------------------
- test sample points
- -------------------------------------
m = test for i in range(len(m.w1)):
m.w1[i].MEAS=train.w1[i].NEWVAL
m.w1[i].FSTATUS = 1
print('w1[str(i)]: '+str(m.w1[i].MEAS))
for i in range(len(m.w2)):
m.w2[i].MEAS=train.w2[i].NEWVAL
m.w2[i].FSTATUS = 1
print('w2[str(i)]: '+str(m.w2[i].MEAS))
for i in range(len(m.w3)):
m.w3[i].MEAS=train.w3[i].NEWVAL
m.w3[i].FSTATUS = 1
print('w3[str(i)]: '+str(m.w3[i].MEAS))
m.inpt.value=np.linspace(-0.1,1.5,100) m.options.IMODE = 2 m.options.SOLVER = 3 m.solve(disp=False)
- -------------------------------------
- un-scale predictions
- -------------------------------------
xp = np.array(test.inpt.value) * x_range + x_min yp = np.array(test.outpt.value) * y_range + y_min
- -------------------------------------
- plot results
- -------------------------------------
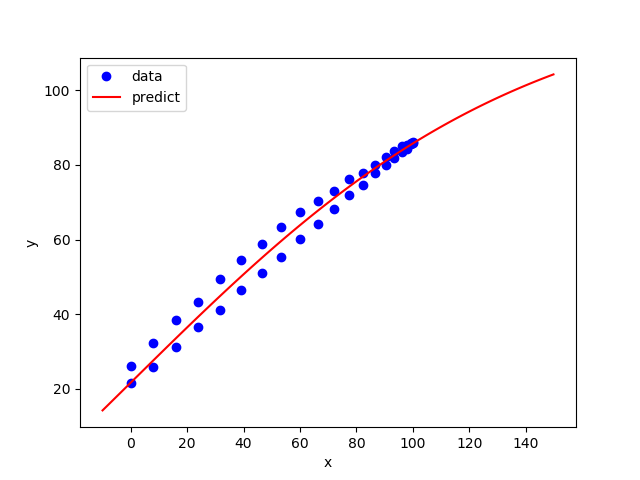
plt.figure() plt.plot(x,y,'bo',label='data') plt.plot(xp,yp,'r-',label='predict') plt.legend(loc='best') plt.ylabel('y') plt.xlabel('x') plt.savefig('tclab_ss_data1.png')
- -------------------------------------
- generate dynamic predictions
- -------------------------------------
m = dyn m.time = np.linspace(0,600,601)
- load neural network parameters
for i in range(len(m.w1)):
m.w1[i].MEAS=train.w1[i].NEWVAL
m.w1[i].FSTATUS = 1
for i in range(len(m.w2)):
m.w2[i].MEAS=train.w2[i].NEWVAL
m.w2[i].FSTATUS = 1
for i in range(len(m.w3)):
m.w3[i].MEAS=train.w3[i].NEWVAL
m.w3[i].FSTATUS = 1
- doublet test
Qd = np.zeros(601) Qd[10:200] = 80 Qd[200:400] = 20 Qd[400:] = 50 Q = m.Param() Q.value = Qd
- scaled input
m.inpt.value = (Qd - x_min) / x_range
- define Temperature output
Q0 = 0 # initial heater T0 = 23 # initial temperature
- scaled steady state ouput
T_ss = m.Var(value=T0) m.Equation(T_ss == m.outpt*y_range + y_min)
- dynamic prediction
T = m.Var(value=T0)
- time constant
tau = m.Param(value=120) # determine in a later exercise
- additional model equation for dynamics
m.Equation(tau*T.dt()==-(T-T0)+(T_ss-T0))
- solve dynamic simulation
m.options.IMODE=4 m.solve()
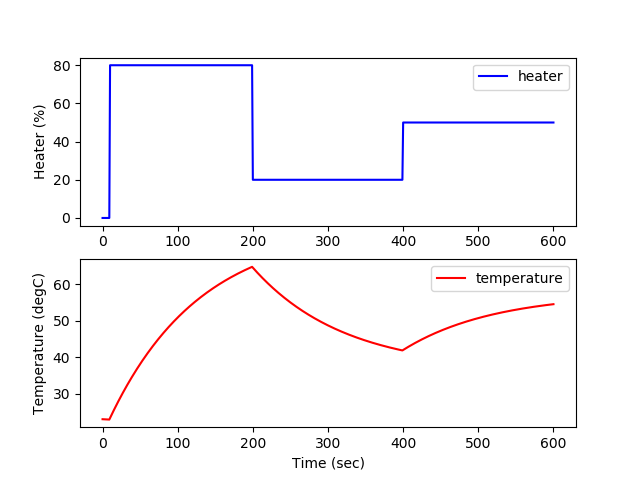
plt.figure() plt.subplot(2,1,1) plt.plot(m.time,Q.value,'b-',label='heater') plt.ylabel('Heater (%)') plt.legend(loc='best') plt.subplot(2,1,2) plt.plot(m.time,T.value,'r-',label='temperature')
- plt.plot(m.time,T_ss.value,'k--',label='target temperature')
plt.ylabel('Temperature (degC)') plt.legend(loc='best') plt.xlabel('Time (sec)') plt.savefig('tclab_dyn_pred.png') plt.show() (:sourceend:) (:divend:)
See also:
- Advanced Control Lab Overview
- TCLab Files on GitHub
- Basic (PID) Control Lab
(:html:) <style> .button {
border-radius: 4px; background-color: #0000ff; border: none; color: #FFFFFF; text-align: center; font-size: 28px; padding: 20px; width: 300px; transition: all 0.5s; cursor: pointer; margin: 5px;
}
.button span {
cursor: pointer; display: inline-block; position: relative; transition: 0.5s;
}
.button span:after {
content: '\00bb'; position: absolute; opacity: 0; top: 0; right: -20px; transition: 0.5s;
}
.button:hover span {
padding-right: 25px;
}
.button:hover span:after {
opacity: 1; right: 0;
} </style> (:htmlend:)