The underlying model or process parameters that describe a system are rarely known exactly. Optimizing a system with an inaccurate model leads to a sub-optimal solution. If the process model includes uncertain parameters that are described by a distribution function or other set of possible process values, this information can be used directly in the optimal control problem to optimize under uncertainty.
Exercise 1
Consider a system that has an uncertain parameter K that is uniformly distributed between 1.0 and 2.0. The process model is
$$10 \frac{dv}{dt} = -v + K p$$
where v is the controlled variable (CV) with target value of 40.0 and p is the manipulated variable (MV) that can be adjusted between 0 and 100. This is a simple first-order dynamic model that relates the adjustable input p (MV) to the target output v (CV). The rate of change of the MV is limited to 40 every seconds. Determine the stochastic optimal control solution by creating 10 instances of the model that randomly determine the value of K. Optimize this set of models to achieve the target CV value of 40, starting from an initial condition of 0.
Solution 1
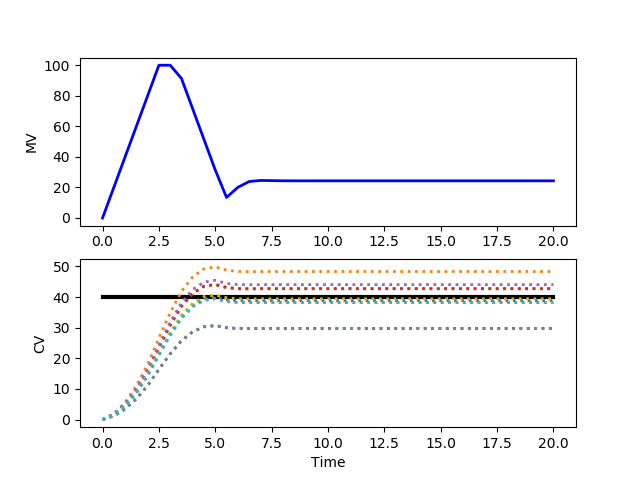
from gekko import GEKKO
import matplotlib.pyplot as plt
# uncertain parameter
n = 10
K = np.random.rand(n)+1.0
m = GEKKO()
m.time = np.linspace(0,20,41)
# manipulated variable
p = m.MV(value=0, lb=0, ub=100)
p.STATUS = 1
p.DCOST = 0.1
p.DMAX = 20
# controlled variable
v = m.Array(m.CV,n)
for i in range(n):
v[i].STATUS = 1
v[i].SP = 40
v[i].TAU = 5
m.Equation(10*v[i].dt() == -v[i] + K[i]*p)
# solve optimal control problem
m.options.IMODE = 6
m.options.CV_TYPE = 2
m.solve()
# plot results
plt.figure()
plt.subplot(2,1,1)
plt.plot(m.time,p.value,'b-',lw=2)
plt.ylabel('MV')
plt.subplot(2,1,2)
plt.plot([0,m.time[-1]],[40,40],'k-',lw=3)
for i in range(n):
plt.plot(m.time,v[i].value,':',lw=2)
plt.ylabel('CV')
plt.xlabel('Time')
plt.show()
Exercise 2
Consider a system that has an uncertain delay that is uniformly distributed between 1.0 and 5.0. The process model is
$$2 \frac{dv}{dt} = -v + p (t-\theta)$$
where v is the controlled variable (CV) with target range between 38.0 and 40.0, p is the manipulated variable (MV) that can be adjusted between 0 and 100, and `\theta` is the delay. This is a simple first-order dynamic model that relates the adjustable input p (MV) to the target output v (CV). The rate of change of the MV is limited to 40 every seconds. Determine the stochastic optimal control solution by creating 6 instances of the model that randomly determine the delay. Optimize this set of models to achieve the target CV value of between 38 and 40, starting from an initial condition of 0.
Solution 2
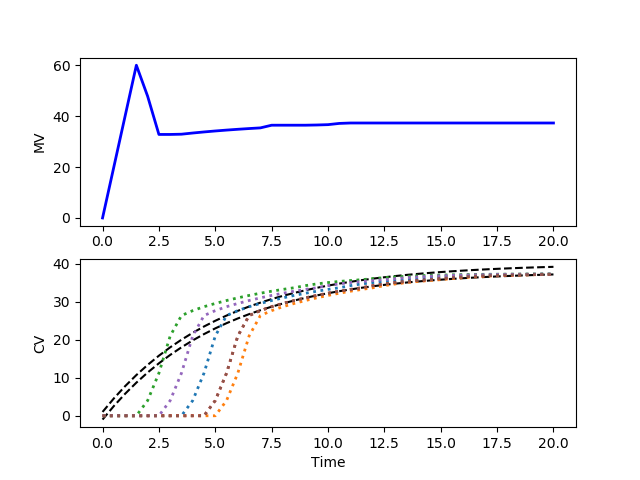
from gekko import GEKKO
import matplotlib.pyplot as plt
# uncertain delay instances
n = 6
m = GEKKO()
m.time = np.linspace(0,20,41)
# manipulated variable
p = m.MV(value=0, lb=0, ub=100)
p.STATUS = 1
p.DCOST = 0.1
p.DMAX = 20
# controlled variable
v = m.Array(m.CV,n)
d = m.Array(m.Var,n)
for i in range(n):
delay = np.random.randint(1,11)
v[i].STATUS = 1
v[i].SPHI = 40
v[i].SPLO = 38
v[i].TAU = 5
v[i].TR_INIT = 1
m.delay(p,d[i],delay)
m.Equation(2*v[i].dt()==-v[i]+d[i])
# solve optimal control problem
m.options.IMODE = 6
m.options.CV_TYPE = 1
m.solve()
# get additional solution information
import json
with open(m.path+'//results.json') as f:
results = json.load(f)
# plot results
plt.figure()
plt.subplot(2,1,1)
plt.plot(m.time,p.value,'b-',lw=2)
plt.ylabel('MV')
plt.subplot(2,1,2)
plt.plot(m.time,results['v1.tr_hi'],'k--')
plt.plot(m.time,results['v1.tr_lo'],'k--')
for i in range(n):
plt.plot(m.time,v[i].value,':',lw=2)
plt.ylabel('CV')
plt.xlabel('Time')
plt.show()