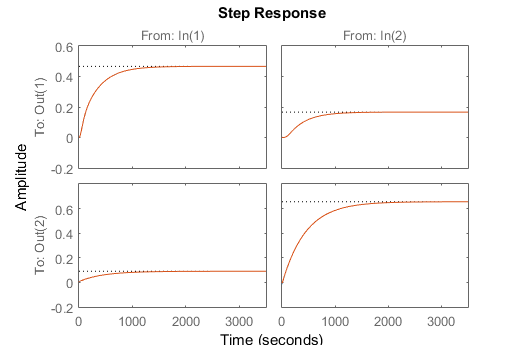
MIMO Model Identification
Main.ModelIdentification History
Hide minor edits - Show changes to markup
m = GEKKO(remote=False) # remote=True for MacOS
m = GEKKO(remote=False)
m = GEKKO(remote=False)
m = GEKKO(remote=False) # remote=True for MacOS
yp,a,b,c = m.sysid(t,u,y,na,nb)
yp,p,K = m.sysid(t,u,y,na,nb,diaglevel=1)
(:toggle hide gekko_step button show="Python TCLab MIMO ID with Step Test Validation":) (:div id=gekko_step:) (:source lang=python:) from gekko import GEKKO import numpy as np import pandas as pd import matplotlib.pyplot as plt
- load data and parse into columns
url = 'http://apmonitor.com/do/uploads/Main/tclab_dyn_data2.txt' data = pd.read_csv(url) t = data['Time'] u = data'H1','H2'? y = data'T1','T2'?
- generate time-series model
m = GEKKO(remote=False)
- system identification
na = 3 # output coefficients nb = 4 # input coefficients yp,p,K = m.sysid(t,u,y,na,nb)
plt.figure() plt.subplot(2,1,1) plt.plot(t,u) plt.legend([r'$H_1$',r'$H_2$']) plt.ylabel('MVs') plt.subplot(2,1,2) plt.plot(t,y) plt.plot(t,yp) plt.legend([r'$T_{1meas}$',r'$T_{2meas}$', r'$T_{1pred}$',r'$T_{2pred}$']) plt.ylabel('CVs') plt.xlabel('Time') plt.savefig('sysid.png')
- step test model
yc,uc = m.arx(p)
- steady state initialization
m.options.IMODE = 1 m.solve(disp=False)
- dynamic simulation (step tests)
m.time = np.linspace(0,240,241) m.options.TIME_SHIFT=0 m.options.IMODE = 4 m.solve(disp=False)
plt.figure()
- step for first MV (Heater 1)
uc[0].value = np.zeros(len(m.time)) uc[0].value[5:] = 100 uc[1].value = np.zeros(len(m.time)) m.solve(disp=False)
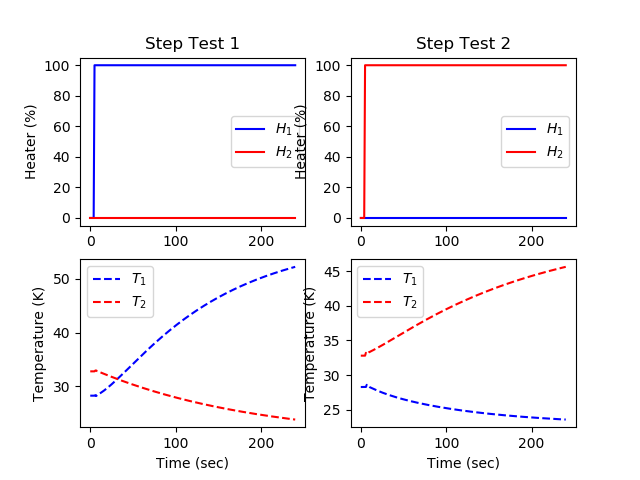
plt.subplot(2,2,1) plt.title('Step Test 1') plt.plot(m.time,uc[0].value,'b-',label=r'$H_1$') plt.plot(m.time,uc[1].value,'r-',label=r'$H_2$') plt.ylabel('Heater (%)') plt.legend() plt.subplot(2,2,3) plt.plot(m.time,yc[0].value,'b--',label=r'$T_1$') plt.plot(m.time,yc[1].value,'r--',label=r'$T_2$') plt.ylabel('Temperature (K)') plt.xlabel('Time (sec)') plt.legend()
- step for second MV (Heater 2)
uc[0].value = np.zeros(len(m.time)) uc[1].value = np.zeros(len(m.time)) uc[1].value[5:] = 100 m.solve(disp=False) plt.subplot(2,2,2) plt.title('Step Test 2') plt.plot(m.time,uc[0].value,'b-',label=r'$H_1$') plt.plot(m.time,uc[1].value,'r-',label=r'$H_2$') plt.ylabel('Heater (%)') plt.legend() plt.subplot(2,2,4) plt.plot(m.time,yc[0].value,'b--',label=r'$T_1$') plt.plot(m.time,yc[1].value,'r--',label=r'$T_2$') plt.ylabel('Temperature (K)') plt.xlabel('Time (sec)') plt.legend()
plt.show() (:sourceend:) (:divend:)
Solution
Solution (Excel, MATLAB, Python)
Solution (GEKKO Python)
(:toggle hide gekko_mimo button show="Python TCLab MIMO ID":) (:div id=gekko_mimo:) (:source lang=python:) from gekko import GEKKO import pandas as pd import matplotlib.pyplot as plt
- load data and parse into columns
url = 'http://apmonitor.com/do/uploads/Main/tclab_dyn_data2.txt' data = pd.read_csv(url) t = data['Time'] u = data'H1','H2'? y = data'T1','T2'?
- generate time-series model
m = GEKKO(remote=False)
- system identification
na = 2 # output coefficients nb = 2 # input coefficients yp,a,b,c = m.sysid(t,u,y,na,nb)
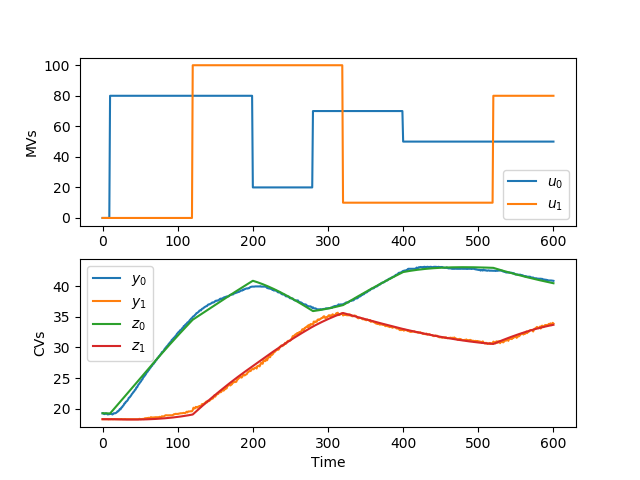
plt.figure() plt.subplot(2,1,1) plt.plot(t,u) plt.legend([r'$u_0$',r'$u_1$']) plt.ylabel('MVs') plt.subplot(2,1,2) plt.plot(t,y) plt.plot(t,yp) plt.legend([r'$y_0$',r'$y_1$',r'$z_0$',r'$z_1$']) plt.ylabel('CVs') plt.xlabel('Time') plt.savefig('sysid.png') plt.show() (:sourceend:) (:divend:)
References
- Nikbakhsh, S., Hedengren, J.D., Darby, M., Udy, J., Constrained Model Identification Using Open-Equation Nonlinear Optimization, AIChE Spring Meeting, Houston, TX, April 2016. Presentation Abstract
In class exercise
The following data set was generated in class from two voltage inputs (u) that changed the temperature (x) of two thermisters.
The following data set was generated in class from two voltage inputs (u) that changed the temperature (x) of two thermistors from the Arduino Lab.
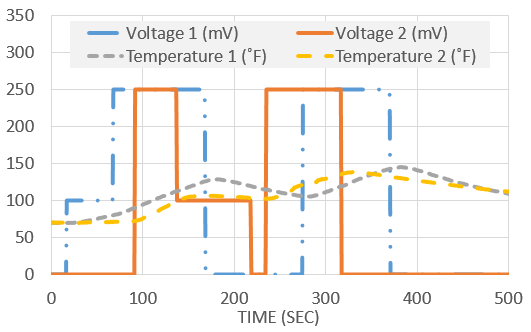

Determine a linear dynamic model that best describes the input to output relationship between voltage and temperature. Compute the steady state gain for each input to output relationship.
Determine a linear dynamic model that best describes the input to output relationship between voltage and temperature. Compute the steady state gain for each input to output relationship. Data and example script files are posted above in Excel and MATLAB.
(:title MIMO Model Identification:) (:keywords dynamic data, model identification, validation, differential, algebraic, tutorial, Simulink:) (:description Multiple input, multiple output model identification for dynamic and empirical identification with an example exercise in Excel, MATLAB, and Python.:)
Multiple Input, Multiple Output (MIMO) systems can be empirically described by several linear dynamic system models. MIMO systems are more complicated than Single Input, Single Output (SISO) systems because of several factors including multivariate interaction, potential co-linearity of inputs, and large data processing requirements. Some common MIMO model forms include:
- Discrete transfer functions (z or q - Time series)
- Continuous transfer functions (s - Laplace variables)
- State space (A,B,C,D - time domain, linear differential equations)
Model identification in these forms typically involves fitting unknown coefficients in the model followed by an analysis to determine how many parameters are statistically significant.
Exercise
The following data set was generated in class from two voltage inputs (u) that changed the temperature (x) of two thermisters.

Determine a linear dynamic model that best describes the input to output relationship between voltage and temperature. Compute the steady state gain for each input to output relationship.
Solution
In class exercise