Dynamic Estimation Introduction
Main.DynamicEstimation History
Show minor edits - Show changes to markup

(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/0LV5yViXML8" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe> (:htmlend:)

 Dynamic Parameter Estimation Notebook |
Dynamic Parameter Estimation Notebook |  Google Colab
Google Colab Dynamic Parameter Estimation Notebook |
Dynamic Parameter Estimation Notebook |  Google Colab
Google Colab Solution Notebook |
Solution Notebook |  Google Colab
Google Colab Solution Notebook |
Solution Notebook |  Google Colab
Google Colab Template Notebook |
Template Notebook |  Google Colab
Google ColabExamples 1-3 Solutions Notebook
 Solution Notebook |
Solution Notebook |  Google Colab
Google Colab Dynamic Parameter Estimation Notebook |
Dynamic Parameter Estimation Notebook |  Google Colab
Google Colab(:divend:)
(:divend:)
Examples 1-3 Solutions Notebook
 Solution Notebook |
Solution Notebook |  Google Colab
Google ColabExamples 1-3 Starting Notebook
 Template Notebook |
Template Notebook |  Google Colab
Google ColabExamples 1-3 Solutions Notebook
 Solution Notebook |
Solution Notebook |  Google Colab
Google ColabEstimate the parameter `a,b,c,d` in the differential equation:
Estimate the parameters `a,b,c,d` in the differential equation:
Objective: Minimize the difference between the measured velocity and predicted velocity by adjusting parameters K and b.
Objective: Minimize the difference between the measured velocity (v_meas) and predicted velocity (v) by adjusting parameters K (gain) and b (resistive coefficient). The vehicle pedal position (p) is measured over a time span of 1 minute and recorded as p_meas.
p = [0,0,0,100,100,100,100,100,100,100,100,100,100] v = [0,0,0,0,18.13,39.35,59.34,75.34,86.47,93.28,96.98,98.89,99.67]
p_meas = [0,0,0,100,100,100,100,100,100,100,100,100,100] v_meas = [0,0,0,0,18.13,39.35,59.34,75.34,86.47,93.28,96.98,98.89,99.67]
Estimate the values of K and b that minimize the difference between the measured and predicted velocity.
time = [0,1,2,3,5,8,12,17,23,30,38,48,60] p = [0,0,0,100,100,100,100,100,100,100,100,100,100] v = [0,0,0,0,18.13,39.35,59.34,75.34,86.47,93.28,96.98,98.89,99.67] mass = 500 kg K = unknown gain (m/s-%pedal) b = unknown resistive coefficient (N-s/m)
$$mass \frac{dv}{dt}+b\,v=K\,b\,p$$
 Video Solution
Video Solution Excel, MATLAB, and Simulink Video Solution
Excel, MATLAB, and Simulink Video Solution Estimate parameters in Excel, MATLAB, and Simulink with Video Solution
Estimate parameters in Excel, MATLAB, and Simulink with Video Solution Video Solution
Video Solution(:toggle hide solution1 button show="Show GEKKO Solution":)
Objective: Minimize the difference between the measured velocity and predicted velocity by adjusting parameters K and b.
(:toggle hide solution1 button show="Show Python GEKKO Solution":)
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/umxAfu44kWo?rel=0" frameborder="0" allowfullscreen></iframe> (:htmlend:)
 Estimate parameters in Excel, MATLAB, and Simulink with Video Solution
Estimate parameters in Excel, MATLAB, and Simulink with Video Solution(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/umxAfu44kWo?rel=0" frameborder="0" allowfullscreen></iframe> (:htmlend:)
Example 2
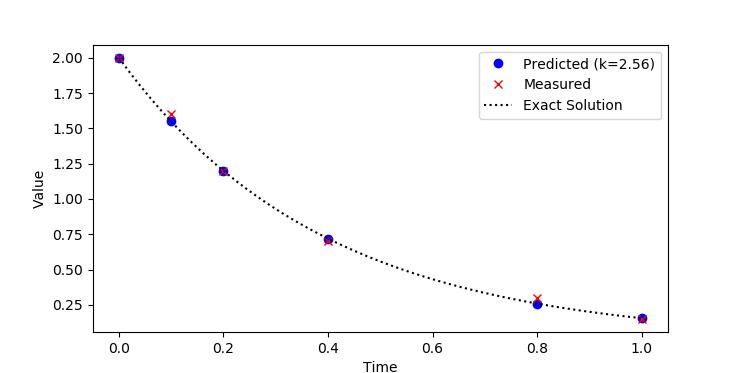
Estimate the parameter `k` in the exponential decay equation:
$$\frac{dx}{dt} = -k\,x$$
by minimizing the error between the predicted and measured `x` values. The `x` values are measured at the following time intervals.
(:toggle hide solution1 button show="Show GEKKO Solution":) (:div id=solution1:)
t_data = [0, 0.1, 0.2, 0.4, 0.8, 1] x_data = [2.0, 1.6, 1.2, 0.7, 0.3, 0.15] (:sourceend:)
Use an initial condition of `x=2` that matches the data. Verify the solution of `x` with the analytic expression `x(t)=2 exp(-k t)`.
(:toggle hide solution3 button show="Show GEKKO Solution":) (:div id=solution3:)
(:source lang=python:)
t_data = [0, 0.1, 0.2, 0.4, 0.8, 1] x_data = [2.0, 1.6, 1.2, 0.7, 0.3, 0.15]
m = GEKKO(remote=False) m.time = t_data x = m.CV(value=x_data); x.FSTATUS = 1 # fit to measurement k = m.FV(); k.STATUS = 1 # adjustable parameter m.Equation(x.dt()== -k * x) # differential equation
m.options.IMODE = 5 # dynamic estimation m.options.NODES = 5 # collocation nodes m.solve(disp=False) # display solver output k = k.value[0]
import matplotlib.pyplot as plt # plot solution plt.plot(m.time,x.value,'bo', label='Predicted (k=str(np.round(k,2)))') plt.plot(m.time,x_data,'rx',label='Measured')
- plot exact solution
t = np.linspace(0,1); xe = 2*np.exp(-k*t) plt.plot(t,xe,'k:',label='Exact Solution') plt.legend() plt.xlabel('Time'), plt.ylabel('Value') plt.show()
m = GEKKO()
m.time = [0,1,2,3,5,8,12,17,23,30,38,48,60] p_meas = [0,0,0,100,100,100,100, 100,100,100,100,100,100] v_meas = [0,0,0,0,18.13,39.35,59.34,75.34, 86.47,93.28,96.98,98.89,99.67]
mass = 500 # kg
b = m.FV(20,lb=1e-5,ub=100) # resistive coefficient (N-s/m) K = m.FV(0.8) # gain (m/s-%pedal) b.STATUS=1; K.STATUS=1 # adjustable by optimizer
p = m.Param(p_meas,lb=0,ub=100) v = m.CV(v_meas); v.FSTATUS = 1 tau = m.Intermediate(mass/b)
m.Equation(tau*v.dt()==-v + K*p)
m.options.IMODE = 5 m.options.NODES = 3 m.options.SOLVER= 1
m.solve()
print('') print('Solution: ') print('K: ' + str(K.value[0])) print('b: ' + str(b.value[0]))
The approach can also be extended to multiple data sets and when the experimental values are at different times.
(:toggle hide solution3b button show="Show GEKKO Solution":) (:div id=solution3b:)
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/umxAfu44kWo?rel=0" frameborder="0" allowfullscreen></iframe> (:htmlend:)
Example 2
Estimate the parameter `k` in the exponential decay equation:
$$\frac{dx}{dt} = -k\,x$$
by minimizing the error between the predicted and measured `x` values. The `x` values are measured at the following time intervals.
t_data = [0, 0.1, 0.2, 0.4, 0.8, 1] x_data = [2.0, 1.6, 1.2, 0.7, 0.3, 0.15] (:sourceend:)
Use an initial condition of `x=2` that matches the data. Verify the solution of `x` with the analytic expression `x(t)=2 exp(-k t)`.
(:toggle hide solution2 button show="Show GEKKO Solution":) (:div id=solution2:)

(:source lang=python:)
t_data = [0, 0.1, 0.2, 0.4, 0.8, 1] x_data = [2.0, 1.6, 1.2, 0.7, 0.3, 0.15]
m = GEKKO(remote=False) m.time = t_data x = m.CV(value=x_data); x.FSTATUS = 1 # fit to measurement k = m.FV(); k.STATUS = 1 # adjustable parameter m.Equation(x.dt()== -k * x) # differential equation
m.options.IMODE = 5 # dynamic estimation m.options.NODES = 5 # collocation nodes m.solve(disp=False) # display solver output k = k.value[0]
import matplotlib.pyplot as plt # plot solution plt.plot(m.time,x.value,'bo', label='Predicted (k=str(np.round(k,2)))') plt.plot(m.time,x_data,'rx',label='Measured')
- plot exact solution
t = np.linspace(0,1); xe = 2*np.exp(-k*t) plt.plot(t,xe,'k:',label='Exact Solution') plt.legend() plt.xlabel('Time'), plt.ylabel('Value') plt.show() (:sourceend:) (:divend:)
The approach can also be extended to multiple data sets and when the experimental values are at different times.
(:toggle hide solution2b button show="Show GEKKO Solution":) (:div id=solution2b:)

(:source lang=python:) from gekko import GEKKO import numpy as np
(:toggle hide solution4 button show="Show GEKKO Solution":) (:div id=solution4:)
(:toggle hide solution3 button show="Show GEKKO Solution":) (:div id=solution3:)
When the analytic solution is not available (most cases), a method to solve dynamic estimation is by numerically integrating the dynamic model at discrete time intervals, much like measuring a physical system at particular time points. The numerical solution is compared to measured values and the difference is minimized by adjusting parameters in the model. Excel, MATLAB, Python, and Simulink are used in the following example to both solve the differential equations that describe the velocity of a vehicle as well as minimize an objective function.
When the analytic solution is not available (most cases), a method to solve dynamic estimation is by numerically integrating the dynamic model at discrete time intervals, much like measuring a physical system at particular time points. The numerical solution is compared to measured values and the difference is minimized by adjusting parameters in the model.
Example 1
Excel, MATLAB, Python, and Simulink are used in the following example to both solve the differential equations that describe the velocity of a vehicle as well as minimize an objective function.
Example 3
Example 2
Example 4
Example 3
Dynamic estimation algorithms optimize model predictions over a prior time horizon of measurements. These state and parameter values may then be used to update the model for improved forward prediction in time to anticipate future dynamic events. The updated model allows dynamic optimization or control actions with increased confidence.
Example 1
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/eXco8_3MmjI" frameborder="0" allowfullscreen></iframe> (:htmlend:)
Example 2
A method to solve dynamic estimation is by numerically integrating the dynamic model at discrete time intervals, much like measuring a physical system at particular time points. The numerical solution is compared to measured values and the difference is minimized by adjusting parameters in the model. Excel, MATLAB, Python, and Simulink are used in the following example to both solve the differential equations that describe the velocity of a vehicle as well as minimize an objective function.
Dynamic estimation algorithms optimize model predictions over a prior time horizon of measurements. These state and parameter values may then be used to update the model for improved forward prediction in time to anticipate future dynamic events. The updated model improves dynamic optimization or control actions because the model better matches reality. A simple example shows how to estimate parameters in the solution to a differential equation in Excel. In this case, an analytic solution of the differential equation is shown.
When the analytic solution is not available (most cases), a method to solve dynamic estimation is by numerically integrating the dynamic model at discrete time intervals, much like measuring a physical system at particular time points. The numerical solution is compared to measured values and the difference is minimized by adjusting parameters in the model. Excel, MATLAB, Python, and Simulink are used in the following example to both solve the differential equations that describe the velocity of a vehicle as well as minimize an objective function.
Multiple Linear Regression
Objective: Perform multiple linear regression on sample data with two inputs.
For linear regression, find unknown parameters c0-c2 to minimize the difference between measured ym and predicted yp subject to a constraint on the summation of c1 x1.
Data
$$x_1 = [1,2,5,3,2,5,2]$$
$$x_2 = [5,6,7,2,1,3,2]$$
$$y_m = [3,2,3,5,6,7,8]$$
Linear Equation
$$y_p = c_0 + c_1 x_1 + c_2 x_2$$
Constraint
$$0 \le \sum_{i=1}^n c_1 x_{1,i} \le 10$$
Minimize Objective
$$\min_{c} \sum_{i=1}^n \left(y_{m,i}-y_{p,i}\right)^2$$
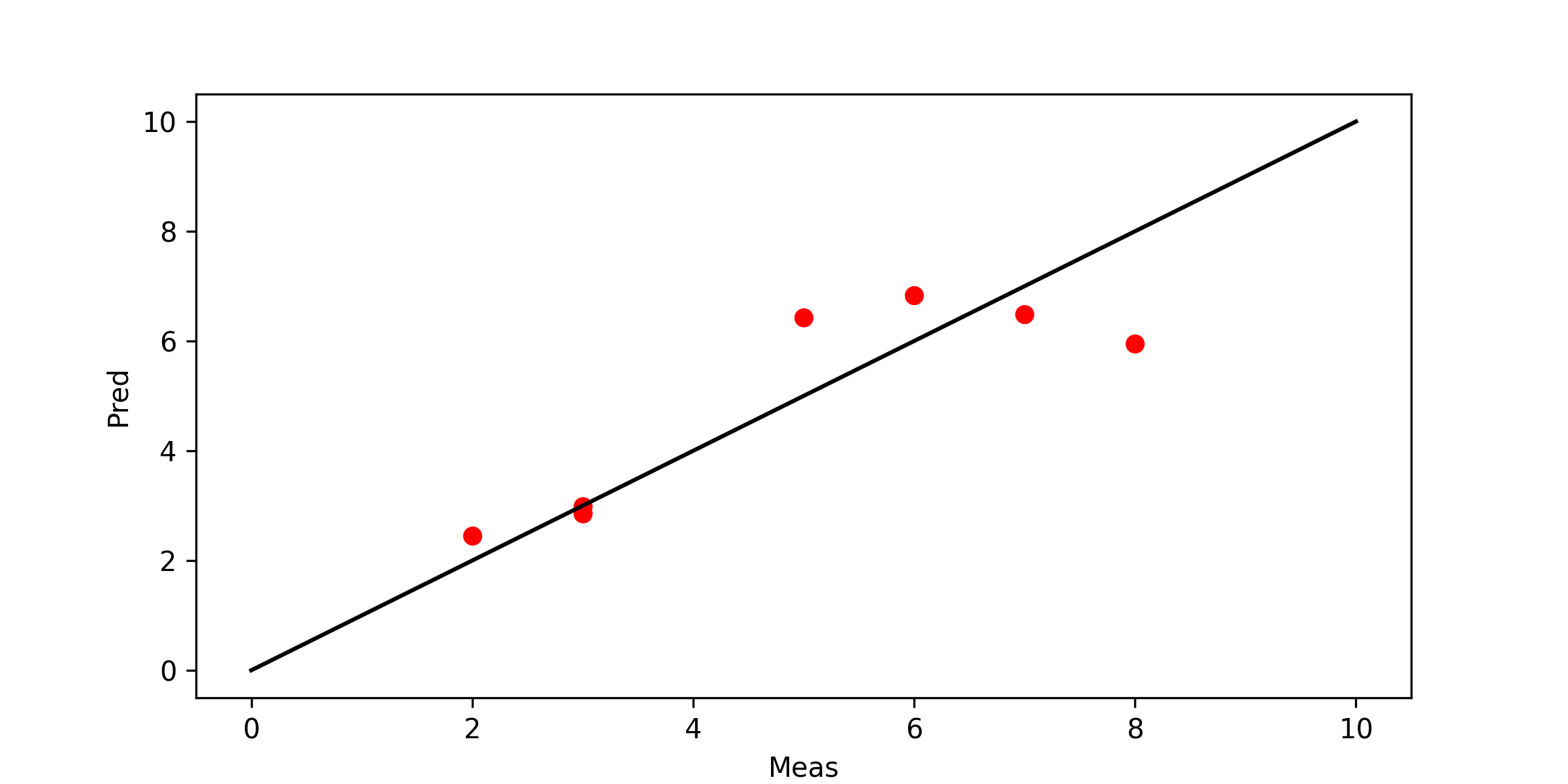
where n is the length of ym and c0-c2 are adjusted to minimize the sum of the squared errors. Report the parameter values and display a plot of the results.
Solution
Python Gekko has a regression mode where the equations are written once and applied over all data rows. The vsum object creates a vertical summation over a column.
(:toggle hide gekko2 button show="Show GEKKO IMODE=2 Solution":) (:div id=gekko2:)
(:source lang=python:) import numpy as np from gekko import GEKKO
- load data
x1 = np.array([1,2,5,3,2,5,2]) x2 = np.array([5,6,7,2,1,3,2]) ym = np.array([3,2,3,5,6,7,8])
- model
m = GEKKO() c = m.Array(m.FV,3) for ci in c:
ci.STATUS=1
x1 = m.Param(value=x1) x2 = m.Param(value=x2) ymeas = m.Param(value=ym) ypred = m.Var() m.Equation(ypred == c[0] + c[1]*x1 + c[2]*x2)
- add constraint on sum(c[1]*x1) with vsum
v1 = m.Var(); m.Equation(v1==c[1]*x1) con = m.Var(lb=0,ub=10); m.Equation(con==m.vsum(v1)) m.Minimize((ypred-ymeas)**2) m.options.IMODE = 2 m.solve() print('Final SSE Objective: ' + str(m.options.objfcnval)) print('Solution') for i,ci in enumerate(c):
print(i,ci.value[0])
- plot solution
import matplotlib.pyplot as plt plt.figure(figsize=(8,4)) plt.plot(ymeas,ypred,'ro') plt.plot([0,10],[0,10],'k-') plt.xlabel('Meas') plt.ylabel('Pred') plt.savefig('results.png',dpi=300) plt.show() (:sourceend:) (:divend:)
It is also possible to write each equation individually for additional control over the regression form. The IMODE=3 option is for optimization problems where each variable, objective term, and equation are written individually. IMODE=2 is more efficient for large-scale problems.
(:toggle hide gekko3 button show="Show GEKKO IMODE=3 Solution":) (:div id=gekko3:)
(:source lang=python:) import numpy as np from gekko import GEKKO
- load data
x1 = np.array([1,2,5,3,2,5,2]) x2 = np.array([5,6,7,2,1,3,2]) ym = np.array([3,2,3,5,6,7,8]) n = len(ym)
- model
m = GEKKO() c = m.Array(m.FV,3) for ci in c:
ci.STATUS=1
yp = m.Array(m.Var,n) for i in range(n):
m.Equation(yp[i]==c[0]+c[1]*x1[i]+c[2]*x2[i])
m.Minimize((yp[i]-ym[i])**2)
- add constraint on sum(c[1]*x1)
s = m.Var(lb=0,ub=10); m.Equation(s==c[1]*sum(x1)) m.options.IMODE = 3 m.solve() print('Final SSE Objective: ' + str(m.options.objfcnval)) print('Solution') for i,ci in enumerate(c):
print(i,ci.value[0])
- plot solution
import matplotlib.pyplot as plt plt.figure(figsize=(8,4)) ypv = [yp[i].value[0] for i in range(n)] plt.plot(ym,ypv,'ro') plt.plot([0,10],[0,10],'k-') plt.xlabel('Meas') plt.ylabel('Pred') plt.savefig('results.png',dpi=300) plt.show() (:sourceend:) (:divend:)
These examples do not have differential equations to describe dynamic systems. For problems with differential equations, use IMODE=5 instead of IMODE=2.
$$0 \le \sum_{i=1}^n \left(c_1 x_{1,i}\right)^2 \le 10$$
$$0 \le \sum_{i=1}^n c_1 x_{1,i} \le 10$$
$$0 \le \sum_{i=1}^n \left(c_1 x_{1,i}\right)^2$ \le 10$$
$$0 \le \sum_{i=1}^n \left(c_1 x_{1,i}\right)^2 \le 10$$
x1 = np.array([1,2,5,3,2,5,2]) x2 = np.array([5,6,7,2,1,3,2]) ym = np.array([3,2,3,5,6,7,8])
{$0 \le \sum_{i=1}^n \left(c_1 x_{1,i}\right)^2$ \le 10}
$$0 \le \sum_{i=1}^n \left(c_1 x_{1,i}\right)^2$ \le 10$$
$$x_1 = [4,5,2,3,-1,1,6,7]$$
$$x_2 = [3,2,3,4, 3,5,2,6]$$
$$y = [0.3,0.8,-0.05,0.1,-0.8,-0.5,0.5,0.65]$$
x1 = np.array([1,2,5,3,2,5,2]) x2 = np.array([5,6,7,2,1,3,2]) ym = np.array([3,2,3,5,6,7,8])
$$x_1 = [1,2,5,3,2,5,2]$$
$$x_2 = [5,6,7,2,1,3,2]$$
$$y_m = [3,2,3,5,6,7,8]$$
$$yp = c_0 + c_1 x_1 + c_2 x_2$$
$$y_p = c_0 + c_1 x_1 + c_2 x_2$$
$$\min_{c} \sum_{i=1}^n \left(ym_i-yp_i\right)^2$$
where n is the length of y and c0-c2 are adjusted to minimize the sum of the squared errors.
Report the parameter values and display a plot of the results.
$$\min_{c} \sum_{i=1}^n \left(y_{m,i}-y_{p,i}\right)^2$$
where n is the length of ym and c0-c2 are adjusted to minimize the sum of the squared errors. Report the parameter values and display a plot of the results.
Python Gekko has a regression mode where the equations are written once and applied over all data rows. The vsum object creates a vertical summation over a column.
It is also possible to write each equation individually for additional control over the regression form. The IMODE=3 option is for optimization problems where each variable, objective term, and equation are written individually. IMODE=2 is more efficient for large-scale problems.
These examples do not have differential equations to describe dynamic systems. For problems with differential equations, use IMODE=5 instead of IMODE=2.
Dynamic estimation algorithms optimize model predictions over a prior time horizon of measurements. These state and parameter values may then be used to update the model for improved forward prediction in time to anticipate future dynamic events. The updated model allows dynamic optimization or control actions with increased confidence.
Dynamic Parameter Estimation Example 1
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/eXco8_3MmjI" frameborder="0" allowfullscreen></iframe> (:htmlend:)
Dynamic Parameter Estimation Example 2
A method to solve dynamic estimation is by numerically integrating the dynamic model at discrete time intervals, much like measuring a physical system at particular time points. The numerical solution is compared to measured values and the difference is minimized by adjusting parameters in the model. Excel, MATLAB, Python, and Simulink are used in the following example to both solve the differential equations that describe the velocity of a vehicle as well as minimize an objective function.
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/umxAfu44kWo?rel=0" frameborder="0" allowfullscreen></iframe> (:htmlend:)
Dynamic Parameter Estimation Example 3
Estimate the parameter `k` in the exponential decay equation:
$$\frac{dx}{dt} = -k\,x$$
by minimizing the error between the predicted and measured `x` values. The `x` values are measured at the following time intervals.
Multiple Linear Regression
Objective: Perform multiple linear regression on sample data with two inputs.
For linear regression, find unknown parameters c0-c2 to minimize the difference between measured ym and predicted yp subject to a constraint on the summation of c1 x1.
Data
$$x_1 = [4,5,2,3,-1,1,6,7]$$
$$x_2 = [3,2,3,4, 3,5,2,6]$$
$$y = [0.3,0.8,-0.05,0.1,-0.8,-0.5,0.5,0.65]$$
Linear Equation
$$yp = c_0 + c_1 x_1 + c_2 x_2$$
Constraint
{$0 \le \sum_{i=1}^n \left(c_1 x_{1,i}\right)^2$ \le 10}
Minimize Objective
$$\min_{c} \sum_{i=1}^n \left(ym_i-yp_i\right)^2$$
where n is the length of y and c0-c2 are adjusted to minimize the sum of the squared errors.
Report the parameter values and display a plot of the results.
Solution

(:toggle hide gekko2 button show="Show GEKKO IMODE=2 Solution":) (:div id=gekko2:)
t_data = [0, 0.1, 0.2, 0.4, 0.8, 1] x_data = [2.0, 1.6, 1.2, 0.7, 0.3, 0.15] (:sourceend:)
Use an initial condition of `x=2` that matches the data. Verify the solution of `x` with the analytic expression `x(t)=2 exp(-k t)`.
(:toggle hide solution3 button show="Show GEKKO Solution":) (:div id=solution3:)

(:source lang=python:)
import numpy as np
t_data = [0, 0.1, 0.2, 0.4, 0.8, 1] x_data = [2.0, 1.6, 1.2, 0.7, 0.3, 0.15]
m = GEKKO(remote=False) m.time = t_data x = m.CV(value=x_data); x.FSTATUS = 1 # fit to measurement k = m.FV(); k.STATUS = 1 # adjustable parameter m.Equation(x.dt()== -k * x) # differential equation
m.options.IMODE = 5 # dynamic estimation m.options.NODES = 5 # collocation nodes m.solve(disp=False) # display solver output k = k.value[0]
- load data
x1 = np.array([1,2,5,3,2,5,2]) x2 = np.array([5,6,7,2,1,3,2]) ym = np.array([3,2,3,5,6,7,8])
- model
m = GEKKO() c = m.Array(m.FV,3) for ci in c:
ci.STATUS=1
x1 = m.Param(value=x1) x2 = m.Param(value=x2) ymeas = m.Param(value=ym) ypred = m.Var() m.Equation(ypred == c[0] + c[1]*x1 + c[2]*x2)
- add constraint on sum(c[1]*x1) with vsum
v1 = m.Var(); m.Equation(v1==c[1]*x1) con = m.Var(lb=0,ub=10); m.Equation(con==m.vsum(v1)) m.Minimize((ypred-ymeas)**2) m.options.IMODE = 2 m.solve() print('Final SSE Objective: ' + str(m.options.objfcnval)) print('Solution') for i,ci in enumerate(c):
print(i,ci.value[0])
- plot solution
import matplotlib.pyplot as plt plt.figure(figsize=(8,4)) plt.plot(ymeas,ypred,'ro') plt.plot([0,10],[0,10],'k-') plt.xlabel('Meas') plt.ylabel('Pred') plt.savefig('results.png',dpi=300) plt.show() (:sourceend:) (:divend:)
(:toggle hide gekko3 button show="Show GEKKO IMODE=3 Solution":) (:div id=gekko3:)
(:source lang=python:)
import matplotlib.pyplot as plt # plot solution plt.plot(m.time,x.value,'bo', label='Predicted (k=str(np.round(k,2)))') plt.plot(m.time,x_data,'rx',label='Measured')
- plot exact solution
t = np.linspace(0,1); xe = 2*np.exp(-k*t) plt.plot(t,xe,'k:',label='Exact Solution') plt.legend() plt.xlabel('Time'), plt.ylabel('Value') plt.show() (:sourceend:) (:divend:)
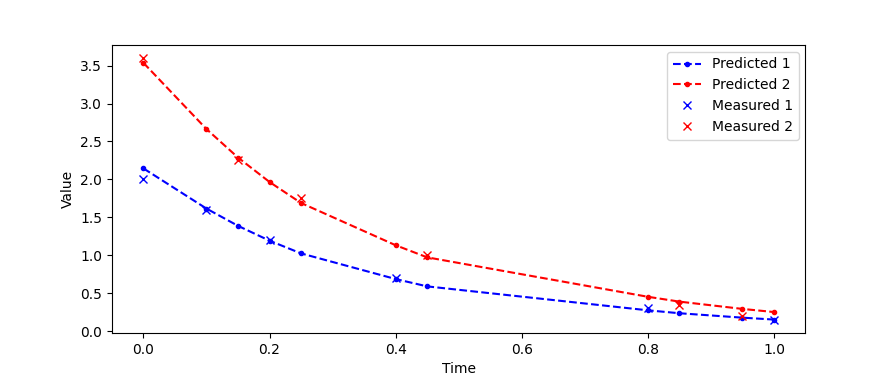
The approach can also be extended to multiple data sets and when the experimental values are at different times.
(:toggle hide solution3b button show="Show GEKKO Solution":) (:div id=solution3b:)

(:source lang=python:)
import numpy as np import pandas as pd
- load data
x1 = np.array([1,2,5,3,2,5,2]) x2 = np.array([5,6,7,2,1,3,2]) ym = np.array([3,2,3,5,6,7,8]) n = len(ym)
- model
m = GEKKO() c = m.Array(m.FV,3) for ci in c:
ci.STATUS=1
yp = m.Array(m.Var,n) for i in range(n):
m.Equation(yp[i]==c[0]+c[1]*x1[i]+c[2]*x2[i])
m.Minimize((yp[i]-ym[i])**2)
- add constraint on sum(c[1]*x1)
s = m.Var(lb=0,ub=10); m.Equation(s==c[1]*sum(x1)) m.options.IMODE = 3 m.solve() print('Final SSE Objective: ' + str(m.options.objfcnval)) print('Solution') for i,ci in enumerate(c):
print(i,ci.value[0])
- plot solution
- data set 1
t_data1 = [0.0, 0.1, 0.2, 0.4, 0.8, 1.00] x_data1 = [2.0, 1.6, 1.2, 0.7, 0.3, 0.15]
- data set 2
t_data2 = [0.0, 0.15, 0.25, 0.45, 0.85, 0.95] x_data2 = [3.6, 2.25, 1.75, 1.00, 0.35, 0.20]
- combine with dataframe join
data1 = pd.DataFrame({'Time':t_data1,'x1':x_data1}) data2 = pd.DataFrame({'Time':t_data2,'x2':x_data2}) data1.set_index('Time', inplace=True) data2.set_index('Time', inplace=True) data = data1.join(data2,how='outer') print(data.head())
- indicate which points are measured
z1 = (data['x1']==data['x1']).astype(int) # 0 if NaN z2 = (data['x2']==data['x2']).astype(int) # 1 if number
- replace NaN with any number (0)
data.fillna(0,inplace=True)
m = GEKKO(remote=False)
- measurements
xm = m.Array(m.Param,2) xm[0].value = data['x1'].values xm[1].value = data['x2'].values
- index for objective (0=not measured, 1=measured)
zm = m.Array(m.Param,2) zm[0].value=z1 zm[1].value=z2
m.time = data.index x = m.Array(m.Var,2) # fit to measurement x[0].value=x_data1[0]; x[1].value=x_data2[0]
k = m.FV(); k.STATUS = 1 # adjustable parameter for i in range(2):
m.free_initial(x[i]) # calculate initial condition
m.Equation(x[i].dt()== -k * x[i]) # differential equations
m.Minimize(zm[i]*(x[i]-xm[i])**2) # objectives
m.options.IMODE = 5 # dynamic estimation m.options.NODES = 2 # collocation nodes m.solve(disp=True) # solve k = k.value[0] print('k = '+str(k))
- plot solution
plt.plot(m.time,x[0].value,'b.--',label='Predicted 1') plt.plot(m.time,x[1].value,'r.--',label='Predicted 2') plt.plot(t_data1,x_data1,'bx',label='Measured 1') plt.plot(t_data2,x_data2,'rx',label='Measured 2') plt.legend(); plt.xlabel('Time'); plt.ylabel('Value') plt.xlabel('Time');
plt.figure(figsize=(8,4)) ypv = [yp[i].value[0] for i in range(n)] plt.plot(ym,ypv,'ro') plt.plot([0,10],[0,10],'k-') plt.xlabel('Meas') plt.ylabel('Pred') plt.savefig('results.png',dpi=300)
Dynamic Parameter Estimation Example 4
Estimate the parameter `a,b,c,d` in the differential equation:
$$\frac{d^3x}{dt^3} = a\frac{d^2x}{dt^2}+b\frac{dx}{dt}+c x+d$$
Dynamic Parameter Estimation
Dynamic estimation algorithms optimize model predictions over a prior time horizon of measurements. These state and parameter values may then be used to update the model for improved forward prediction in time to anticipate future dynamic events. The updated model allows dynamic optimization or control actions with increased confidence.
Example 1
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/eXco8_3MmjI" frameborder="0" allowfullscreen></iframe> (:htmlend:)
Example 2
A method to solve dynamic estimation is by numerically integrating the dynamic model at discrete time intervals, much like measuring a physical system at particular time points. The numerical solution is compared to measured values and the difference is minimized by adjusting parameters in the model. Excel, MATLAB, Python, and Simulink are used in the following example to both solve the differential equations that describe the velocity of a vehicle as well as minimize an objective function.
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/umxAfu44kWo?rel=0" frameborder="0" allowfullscreen></iframe> (:htmlend:)
Example 3
Estimate the parameter `k` in the exponential decay equation:
$$\frac{dx}{dt} = -k\,x$$
by minimizing the error between the predicted and measured `x` values. The `x` values are measured at the following time intervals.
(:source lang=python:) t_data = [0, 0.1, 0.2, 0.4, 0.8, 1] x_data = [2.0, 1.6, 1.2, 0.7, 0.3, 0.15] (:sourceend:)
Use an initial condition of `x=2` that matches the data. Verify the solution of `x` with the analytic expression `x(t)=2 exp(-k t)`.
(:toggle hide solution3 button show="Show GEKKO Solution":) (:div id=solution3:)

(:source lang=python:) from gekko import GEKKO
t_data = [0, 0.1, 0.2, 0.4, 0.8, 1] x_data = [2.0, 1.6, 1.2, 0.7, 0.3, 0.15]
m = GEKKO(remote=False) m.time = t_data x = m.CV(value=x_data); x.FSTATUS = 1 # fit to measurement k = m.FV(); k.STATUS = 1 # adjustable parameter m.Equation(x.dt()== -k * x) # differential equation
m.options.IMODE = 5 # dynamic estimation m.options.NODES = 5 # collocation nodes m.solve(disp=False) # display solver output k = k.value[0]
import numpy as np import matplotlib.pyplot as plt # plot solution plt.plot(m.time,x.value,'bo', label='Predicted (k=str(np.round(k,2)))') plt.plot(m.time,x_data,'rx',label='Measured')
- plot exact solution
t = np.linspace(0,1); xe = 2*np.exp(-k*t) plt.plot(t,xe,'k:',label='Exact Solution') plt.legend() plt.xlabel('Time'), plt.ylabel('Value') plt.show() (:sourceend:) (:divend:)
The approach can also be extended to multiple data sets and when the experimental values are at different times.
(:toggle hide solution3b button show="Show GEKKO Solution":) (:div id=solution3b:)

(:source lang=python:) from gekko import GEKKO import numpy as np import pandas as pd import matplotlib.pyplot as plt
- data set 1
t_data1 = [0.0, 0.1, 0.2, 0.4, 0.8, 1.00] x_data1 = [2.0, 1.6, 1.2, 0.7, 0.3, 0.15]
- data set 2
t_data2 = [0.0, 0.15, 0.25, 0.45, 0.85, 0.95] x_data2 = [3.6, 2.25, 1.75, 1.00, 0.35, 0.20]
- combine with dataframe join
data1 = pd.DataFrame({'Time':t_data1,'x1':x_data1}) data2 = pd.DataFrame({'Time':t_data2,'x2':x_data2}) data1.set_index('Time', inplace=True) data2.set_index('Time', inplace=True) data = data1.join(data2,how='outer') print(data.head())
- indicate which points are measured
z1 = (data['x1']==data['x1']).astype(int) # 0 if NaN z2 = (data['x2']==data['x2']).astype(int) # 1 if number
- replace NaN with any number (0)
data.fillna(0,inplace=True)
m = GEKKO(remote=False)
- measurements
xm = m.Array(m.Param,2) xm[0].value = data['x1'].values xm[1].value = data['x2'].values
- index for objective (0=not measured, 1=measured)
zm = m.Array(m.Param,2) zm[0].value=z1 zm[1].value=z2
m.time = data.index x = m.Array(m.Var,2) # fit to measurement x[0].value=x_data1[0]; x[1].value=x_data2[0]
k = m.FV(); k.STATUS = 1 # adjustable parameter for i in range(2):
m.free_initial(x[i]) # calculate initial condition
m.Equation(x[i].dt()== -k * x[i]) # differential equations
m.Minimize(zm[i]*(x[i]-xm[i])**2) # objectives
m.options.IMODE = 5 # dynamic estimation m.options.NODES = 2 # collocation nodes m.solve(disp=True) # solve k = k.value[0] print('k = '+str(k))
- plot solution
plt.plot(m.time,x[0].value,'b.--',label='Predicted 1') plt.plot(m.time,x[1].value,'r.--',label='Predicted 2') plt.plot(t_data1,x_data1,'bx',label='Measured 1') plt.plot(t_data2,x_data2,'rx',label='Measured 2') plt.legend(); plt.xlabel('Time'); plt.ylabel('Value') plt.xlabel('Time'); plt.show() (:sourceend:) (:divend:)
Example 4
plt.show() (:sourceend:) (:divend:)
The approach can also be extended to multiple data sets and when the experimental values are at different times.
(:toggle hide solution3b button show="Show GEKKO Solution":) (:div id=solution3b:)

(:source lang=python:) from gekko import GEKKO import numpy as np import pandas as pd import matplotlib.pyplot as plt
- data set 1
t_data1 = [0.0, 0.1, 0.2, 0.4, 0.8, 1.00] x_data1 = [2.0, 1.6, 1.2, 0.7, 0.3, 0.15]
- data set 2
t_data2 = [0.0, 0.15, 0.25, 0.45, 0.85, 0.95] x_data2 = [3.6, 2.25, 1.75, 1.00, 0.35, 0.20]
- combine with dataframe join
data1 = pd.DataFrame({'Time':t_data1,'x1':x_data1}) data2 = pd.DataFrame({'Time':t_data2,'x2':x_data2}) data1.set_index('Time', inplace=True) data2.set_index('Time', inplace=True) data = data1.join(data2,how='outer') print(data.head())
- indicate which points are measured
z1 = (data['x1']==data['x1']).astype(int) # 0 if NaN z2 = (data['x2']==data['x2']).astype(int) # 1 if number
- replace NaN with any number (0)
data.fillna(0,inplace=True)
m = GEKKO(remote=False)
- measurements
xm = m.Array(m.Param,2) xm[0].value = data['x1'].values xm[1].value = data['x2'].values
- index for objective (0=not measured, 1=measured)
zm = m.Array(m.Param,2) zm[0].value=z1 zm[1].value=z2
m.time = data.index x = m.Array(m.Var,2) # fit to measurement x[0].value=x_data1[0]; x[1].value=x_data2[0]
k = m.FV(); k.STATUS = 1 # adjustable parameter for i in range(2):
m.free_initial(x[i]) # calculate initial condition
m.Equation(x[i].dt()== -k * x[i]) # differential equations
m.Minimize(zm[i]*(x[i]-xm[i])**2) # objectives
m.options.IMODE = 5 # dynamic estimation m.options.NODES = 2 # collocation nodes m.solve(disp=True) # solve k = k.value[0] print('k = '+str(k))
- plot solution
plt.plot(m.time,x[0].value,'b.--',label='Predicted 1') plt.plot(m.time,x[1].value,'r.--',label='Predicted 2') plt.plot(t_data1,x_data1,'bx',label='Measured 1') plt.plot(t_data2,x_data2,'rx',label='Measured 2') plt.legend(); plt.xlabel('Time'); plt.ylabel('Value') plt.xlabel('Time');
x_data = [2.0,1.6,1.2,0.7,0.3,0.15,0.1, 0.05,0.03,0.02,0.015,0.01]
x_data = [2.0,1.6,1.2,0.7,0.3,0.15,0.1,0.05,0.03,0.02,0.015,0.01]
Use an initial condition of `x=2` that matches the data.
Use an initial condition of `x=2` that matches the data. Create new states `y=dx/dt` and `z=dy/dt` for the higher order derivative terms.
$$\frac{dx}{dt} = y$$ $$\frac{dy}{dt} = z$$ $$\frac{dz}{dt} = az+by+cx+d$$
plt.legend() plt.xlabel('Time'), plt.ylabel('Value') plt.show() (:sourceend:) (:divend:)
Dynamic Parameter Estimation Example 4
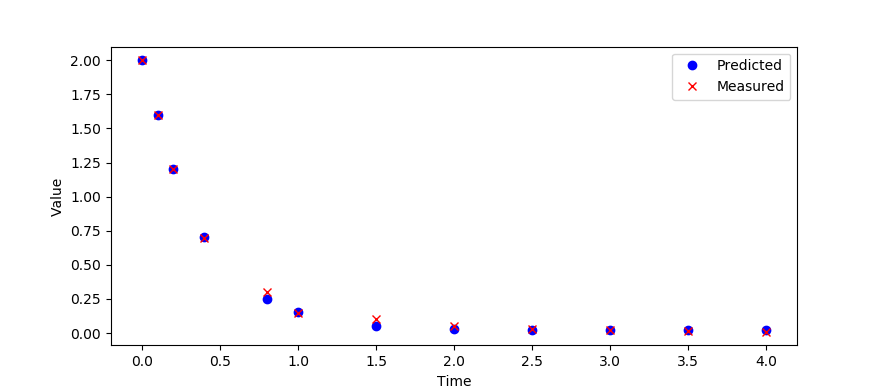
Estimate the parameter `a,b,c,d` in the differential equation:
$$\frac{d^3x}{dt^3} = a\frac{d^2x}{dt^2}+b\frac{dx}{dt}+c x+d$$
by minimizing the error between the predicted and measured `x` values. The `x` values are measured at the following time intervals.
(:source lang=python:) t_data = [0,0.1,0.2,0.4,0.8,1,1.5,2,2.5,3,3.5,4] x_data = [2.0,1.6,1.2,0.7,0.3,0.15,0.1, 0.05,0.03,0.02,0.015,0.01] (:sourceend:)
Use an initial condition of `x=2` that matches the data.
(:toggle hide solution4 button show="Show GEKKO Solution":) (:div id=solution4:)
(:source lang=python:) from gekko import GEKKO
t_data = [0,0.1,0.2,0.4,0.8,1,1.5,2,2.5,3,3.5,4] x_data = [2.0,1.6,1.2,0.7,0.3,0.15,0.1, 0.05,0.03,0.02,0.015,0.01]
m = GEKKO() m.time = t_data
- states
x = m.CV(value=x_data); x.FSTATUS = 1 # fit to measurement y,z = m.Array(m.Var,2,value=0)
- adjustable parameters
a,b,c,d = m.Array(m.FV,4) a.STATUS=1; b.STATUS=1; c.STATUS=1; d.STATUS=1
- differential equation
- Original: x' = a*x + b x' + c x + d
- Transform: y = x'
- z = y'
- z' = a*z + b*y + c*x + d
m.Equations([y==x.dt(),z==y.dt()]) m.Equation(z.dt()==a*z+b*y+c*x+d) # differential equation
m.options.IMODE = 5 # dynamic estimation m.options.NODES = 3 # collocation nodes m.solve(disp=False) # display solver output print(a.value[0],b.value[0],c.value[0],d.value[0])
import matplotlib.pyplot as plt # plot solution plt.plot(m.time,x.value,'bo',label='Predicted') plt.plot(m.time,x_data,'rx',label='Measured')
$$\frac{x}{dt} = -k\,x$$
$$\frac{dx}{dt} = -k\,x$$
Use an initial condition of `x=2` that matches the data. Verify the solution of `x` with the analytic expression `x(t)=2 exp(-k\,t)`.
Use an initial condition of `x=2` that matches the data. Verify the solution of `x` with the analytic expression `x(t)=2 exp(-k t)`.
by matching the predicted `x` to the measured `x` data:
by minimizing the error between the predicted and measured `x` values. The `x` values are measured at the following time intervals.
time = [0, 0.1, 0.2, 0.4, 0.8, 1] x_data = [2.0081, 1.5512, 1.1903, 0.7160, 0.2562, 0.1495]
t_data = [0, 0.1, 0.2, 0.4, 0.8, 1] x_data = [2.0, 1.6, 1.2, 0.7, 0.3, 0.15]
Verify the solution of `x` with the analytic expression `x(t)=exp(-k\,t)`.
Use an initial condition of `x=2` that matches the data. Verify the solution of `x` with the analytic expression `x(t)=2 exp(-k\,t)`.
(:toggle hide solution3 button show="Show GEKKO Solution":) (:div id=solution3:)

(:source lang=python:) from gekko import GEKKO
t_data = [0, 0.1, 0.2, 0.4, 0.8, 1] x_data = [2.0, 1.6, 1.2, 0.7, 0.3, 0.15]
m = GEKKO(remote=False) m.time = t_data x = m.CV(value=x_data); x.FSTATUS = 1 # fit to measurement k = m.FV(); k.STATUS = 1 # adjustable parameter m.Equation(x.dt()== -k * x) # differential equation
m.options.IMODE = 5 # dynamic estimation m.options.NODES = 5 # collocation nodes m.solve(disp=False) # display solver output k = k.value[0]
import numpy as np import matplotlib.pyplot as plt # plot solution plt.plot(m.time,x.value,'bo', label='Predicted (k=str(np.round(k,2)))') plt.plot(m.time,x_data,'rx',label='Measured')
- plot exact solution
t = np.linspace(0,1); xe = 2*np.exp(-k*t) plt.plot(t,xe,'k:',label='Exact Solution') plt.legend() plt.xlabel('Time'), plt.ylabel('Value') plt.show() (:sourceend:) (:divend:)
Dynamic Parameter Estimation Example 3
Estimate the parameter `k` in the exponential decay equation:
$$\frac{x}{dt} = -k\,x$$
by matching the predicted `x` to the measured `x` data:
(:source lang=python:) time = [0, 0.1, 0.2, 0.4, 0.8, 1] x_data = [2.0081, 1.5512, 1.1903, 0.7160, 0.2562, 0.1495] (:sourceend:)
Verify the solution of `x` with the analytic expression `x(t)=exp(-k\,t)`.
Dynamic Parameter Estimation Example
Dynamic Parameter Estimation Example 1
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/eXco8_3MmjI" frameborder="0" allowfullscreen></iframe> (:htmlend:)
Dynamic Parameter Estimation Example 2
<iframe width="560" height="315" src="https://www.youtube.com/embed/y0ERNz5Kms8?rel=0" frameborder="0" allowfullscreen></iframe>
<iframe width="560" height="315" src="https://www.youtube.com/embed/umxAfu44kWo?rel=0" frameborder="0" allowfullscreen></iframe>
Numerical Solution Tutorial for Dynamic Parameter Estimation
Dynamic Parameter Estimation Example
Numerical Estimation Introduction
Numerical Solution Tutorial for Dynamic Parameter Estimation
Numerical Estimation Introduction
A method to solve dynamic estimation is by numerically integrating the dynamic model at discrete time intervals, much like measuring a physical system at particular time points. The numerical solution is compared to measured values and the difference is minimized by adjusting parameters in the model. Excel, MATLAB, Python, and Simulink are used in the following example to both solve the differential equations that describe the velocity of a vehicle as well as minimize an objective function.
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/y0ERNz5Kms8?rel=0" frameborder="0" allowfullscreen></iframe> (:htmlend:)
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/UTxYp0VTe-E?rel=0" frameborder="0" allowfullscreen></iframe> (:htmlend:)
(:title Estimation Introduction:)
(:title Dynamic Estimation Introduction:)
(:title Estimation Introduction:) (:keywords dynamic data, validation, estimation, simulation, modeling language, differential, algebraic, tutorial:) (:description Dynamic estimation for use in real-time or off-line dynamic simulators and controllers:)
Dynamic estimation is a method to align data and model predictions for time-varying systems. Dynamic models and data rarely align perfectly because of several factors including limiting assumptions that were used to build the model, incorrect model parameters, data that is corrupted by measurement noise, instrument calibration problems, measurement delay, and many other factors. All of these factors may cause mismatch between predicted and measured values.
The focus of this section is to develop methods with dynamic optimization to realign model predictions and measured values with the goal of estimating states and parameters. Another focus of this section is to understand model structure that can lead to poorly observable parameters and determine confidence regions for parameter estimates. The uncertainty analysis serves to not only predict unmeasured quantities but also to relate a confidence in those predictions.
Dynamic estimation algorithms optimize model predictions over a prior time horizon of measurements. These state and parameter values may then be used to update the model for improved forward prediction in time to anticipate future dynamic events. The updated model allows dynamic optimization or control actions with increased confidence.