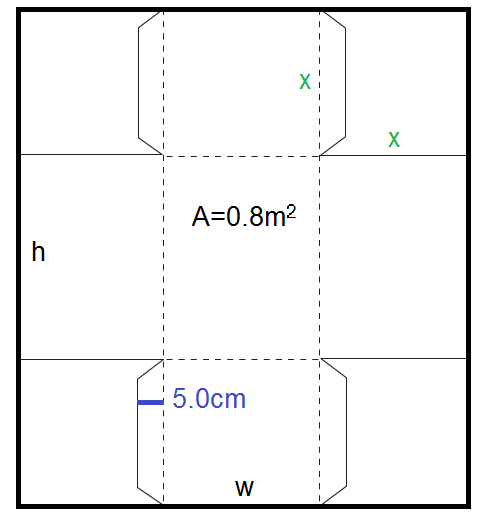
A piece of cardboard with a total area of 0.8m2 is to be made into an open-top box by first removing the corners and then by folding the box sides up and securing the tabs to the adjacent box side. The starting cardboard sheet has height h and width w. When cut and folded, the box has a width of w-2x, a length of h-2x, and a height of x. In order to properly secure the tabs to the adjacent box side, the width of the tab must be 5 centimeters (0.05m). The objective is to maximize the volume of the box by choosing an appropriate value of x (the height of the box) and w (the starting width of the cardboard sheet).
Download Sample Python Code
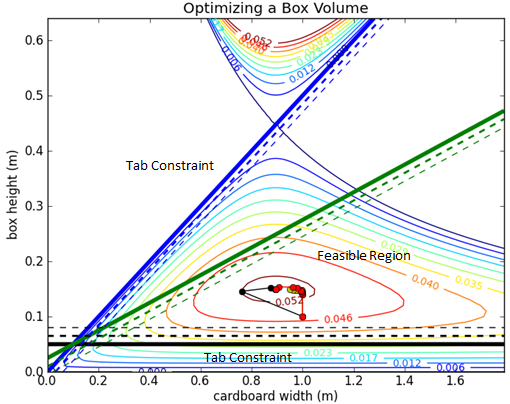
Python source code solves the box optimization problem with Newton's method, a quasi-Newton's method (BFGS), a steepest descent approach, and a conjugate gradient method. After the script executes, a figure appears that shows a contour plot of the solution with a graphical depiction of the progress of each method.
Python Gekko Solution
m = GEKKO()
tabs = 5.0 / 100 # m = cm * (1m/100cm)
Area = 0.8 # m^2
w = m.Var(lb=0) # width of the cardboard piece
x = m.Var(lb=0) # length of cut-out
h = m.Intermediate(Area / w) # Area = w h
box_width = m.Intermediate(w - 2 * x)
box_length = m.Intermediate(h - 2 * x)
box_height = m.Intermediate(x)
box_width_with_tabs = m.Intermediate(box_width + 2 * tabs)
Volume = m.Intermediate(box_width * box_length * box_height)
# upper constraint for box width with tabs
m.Equation(box_width_with_tabs < w)
# lower constraint for box width with tabs
m.Equations([box_width > 0,box_length > 0,Volume>0.01])
m.Maximize(Volume)
m.solve()
print('width = ' + str(w.value[0]))
print('length = ' + str(h.value[0]))
print('height = ' + str(x.value[0]))
print('volume = ' + str(Volume.value[0]))
Test your knowledge with a Quiz on Box Folding Optimization
