Ethanol Bioreactor

Bioreactors create a biologically active environment for the production of chemicals. A bioreactor is a vessel where organisms are grown and preferential products are produced by controlling the feed and temperature. Bioreactors can either be aerobic or anaerobic.

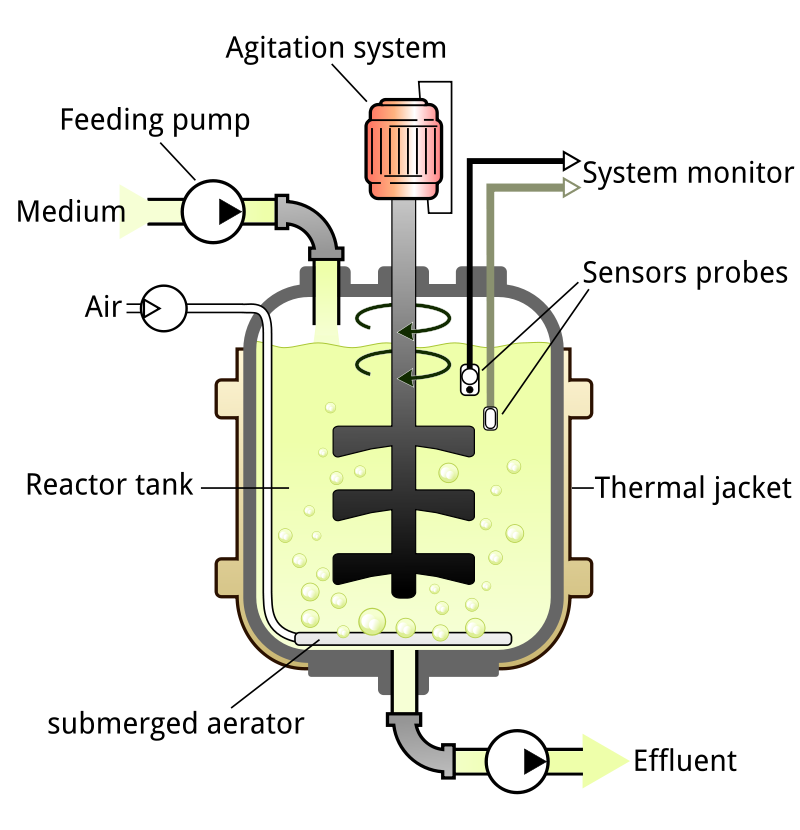
One particular batch bioreactor is fed at varying rates throughout the batch process to produce ethanol. Algebraic equations define the heat generation, rate constants, volume, and other factors used in the model. Symbols and units are defined in the source code.

Growth Rate

$$\mu=\mu_{\max} \frac{{S}}{{K}_{{SX}}+{S}} \frac{{O}_{{liq}}}{{K}_{{OX}}+{O}_{{liq}}}\left(1-\frac{{P}}{{P}_{\max}}\right) \frac{1}{1+\exp (-(100-{S}))}$$

$$\mu_{\max}=\left[\left({a}_1\left({~T}-{k}_1\right)\right)\left(1-\exp \left({b}_1\left({~T}-{k}_2\right)\right)\right)\right]^2$$

$${P}_{\max}={P}_{\operatorname{maxb}}+\frac{{P}_{\operatorname{maxT}}}{1-\exp \left(-{b}_2\left({~T}-{k}_3\right)\right)}$$

$${q}_{{P}}={a}_{{P}} \mu+{b}_{{P}}$$

Non-Growth Ethanol Production

$${b}_{{P}}={c}_1 \exp \left(-\frac{{A}_{{P} 1}}{{~T}}\right)-{c}_2 \exp \left(-\frac{{A}_{{P} 2}}{{~T}}\right)$$

Ethanol Consumption Rate

$${q}_{{S}}=\frac{\mu}{{Y}_{{XS}}}+\frac{{q}_{{P}}}{{Y}_{{PS}}}$$

Oxygen Consumption Rate

$${q}_{{O}}=\frac{{q}_{{O}, \max}}{{Y}_{{Xo}}} \frac{{O}_{{liq}}}{{K}_{{OX}}+{O}_{{liq}}}$$

Biological Cell Mass Deactivation Rate

$${K}_{{d}}={K}_{{db}}+\frac{{K}_{{dT}}}{1+\exp \left(-{b}_3\left({~T}-{k}_4\right)\right)}$$

Oxygen Saturation Concentration

$${O}^*=\frac{{zO}_{{gas}} {RT}}{{K}_{{H}}}$$

Oxygen Mass Transfer Coefficient

$${k}_{l} {a}=\left({k}_{l} {a}\right)_0(1.2)^{{T}-20}$$

Liquid and Vapor Volumes

$${V}_{{l}}+{V}_{{g}}={V}$$

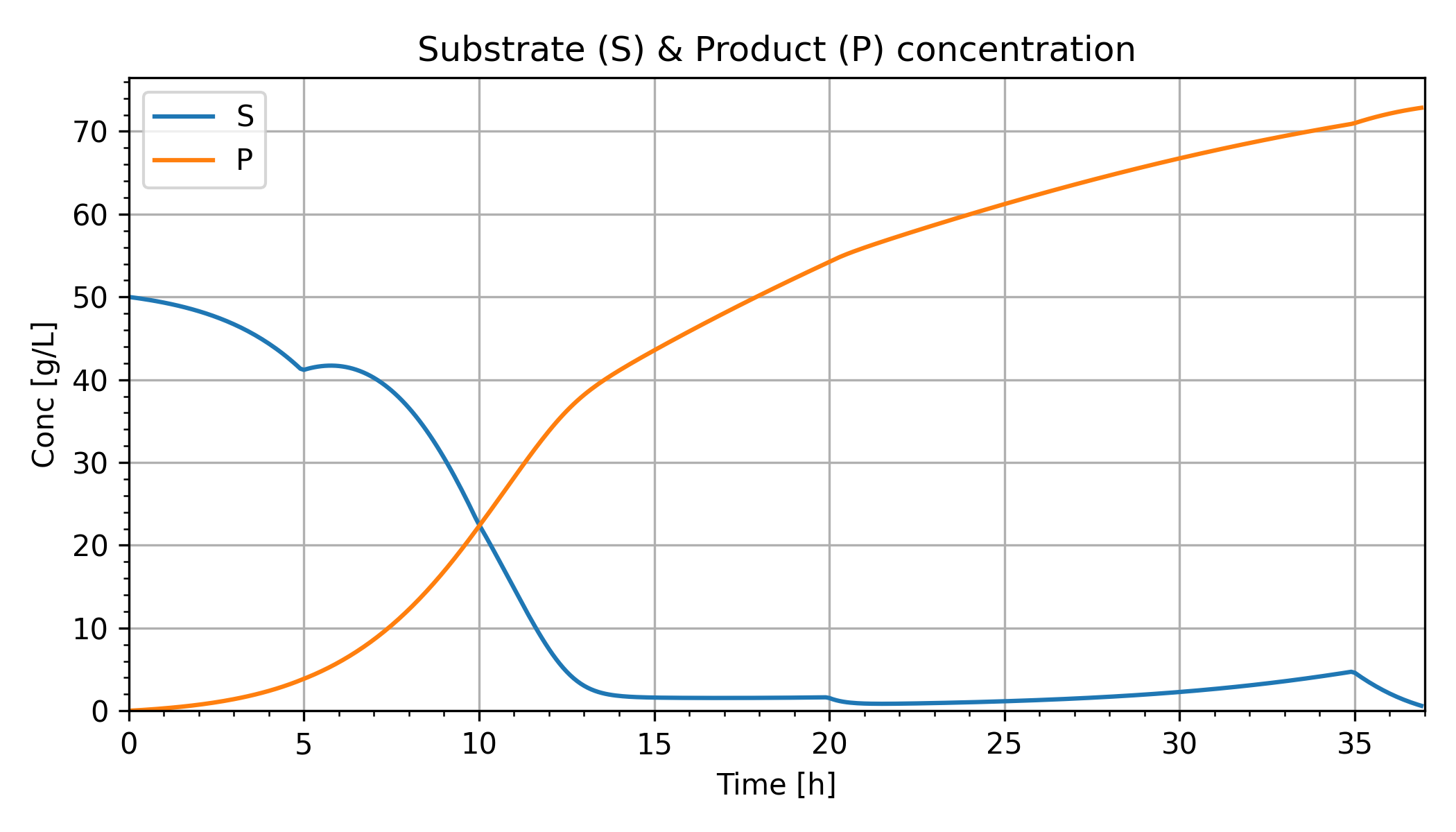
Differential equations are from material, species, and energy balances. The differential equations relate the input flow and substrate concentrations to ethanol production.

Liquid Volume

$$\frac{d V_1}{d t}=Q_{i n}-Q_e$$

Total Cell Mass

$$\frac{{dX}}{{dt}}=\frac{{Q}_{{in}}}{{V}_1}\left({X}_{{t}, {in}}-{X}_{{t}}\right)+\mu {X}_{{v}}$$

Total Biologically Active Cell Mass

$$\frac{d X_v}{d t}=\frac{Q_{i n}}{V_1}\left(X_{v, i n}-X_v\right)+\left(\mu-K_d\right) X_v$$

Glucose (Substrate) Concentration

$$\frac{{dS}}{{dt}}=\frac{{Q}_{{in}}}{{V}_{{l}}}\left({S}_{{in}}-{S}\right)-{q}_{{S}} {X}_{{v}}$$

Ethanol (Product) Concentration

$$\frac{{dP}}{{dt}}=\frac{{Q}_{{in}}}{{V}_1}\left({P}_{{in}}-{P}\right)+{q}_{{P}} X_{{v}}$$

Liquid Oxygen Concentration

$$\frac{{dO}_{liq}}{{dt}}=\frac{{Q}_{{in}}}{{V}_{{l}}}\left({O}^*-{O}_{{liq}}\right)+\left({k}_{{l}} {a}\right)\left({O}^*-{O}_{{liq}}\right)-{qo}_{{o}} {X}_{{v}}$$

Gas Oxygen Concentration

$$\frac{d O_{{gas}}}{d t}=\frac{F_{{air}}}{V_g}\left(O_{{gas}, { in}}-O_{{gas}}\right)-\frac{V_l\left(k_l a\right)}{V_g}\left(O^*-O_{{liq}}\right)+O_{{gas}} \frac{Q_{{in}}-Q_e}{V_g}$$

Bioreactor Temperature

$$\frac{{dT}}{{dt}}=\frac{{Q}_{{in}}}{{V}_{{l}}}\left({T}_{{in}}-{T}\right)-\frac{{T}_{{ref}}}{{V}_{{l}}}\left({Q}_{{in}}-{Q}_{{e}}\right)+\frac{{q}_{{o}} {X}_{{v}} \Delta {H}}{{MW}_{{O}} \rho {C}_{{p}, {br}}}-\frac{{K}_{{T}} {A}_{{T}}\left({T}-{T}_{{c}}\right)}{{V}_{{l}} \rho {C}_{{p}, {br}}}$$

Cooling Agent Temperature

$$\frac{{dT}_{{c}}}{{dt}}=\frac{{F}_{{c}}}{{V}_{{cj}}}\left({T}_{{c}, {in}}-{T}_{{c}}\right)+\frac{{K}_{{T}} {A}_{{T}}\left({T}-{T}_{{c}}\right)}{{V}_{{cj}} \rho_{{c}} {C}_{{p}, {c}}}$$

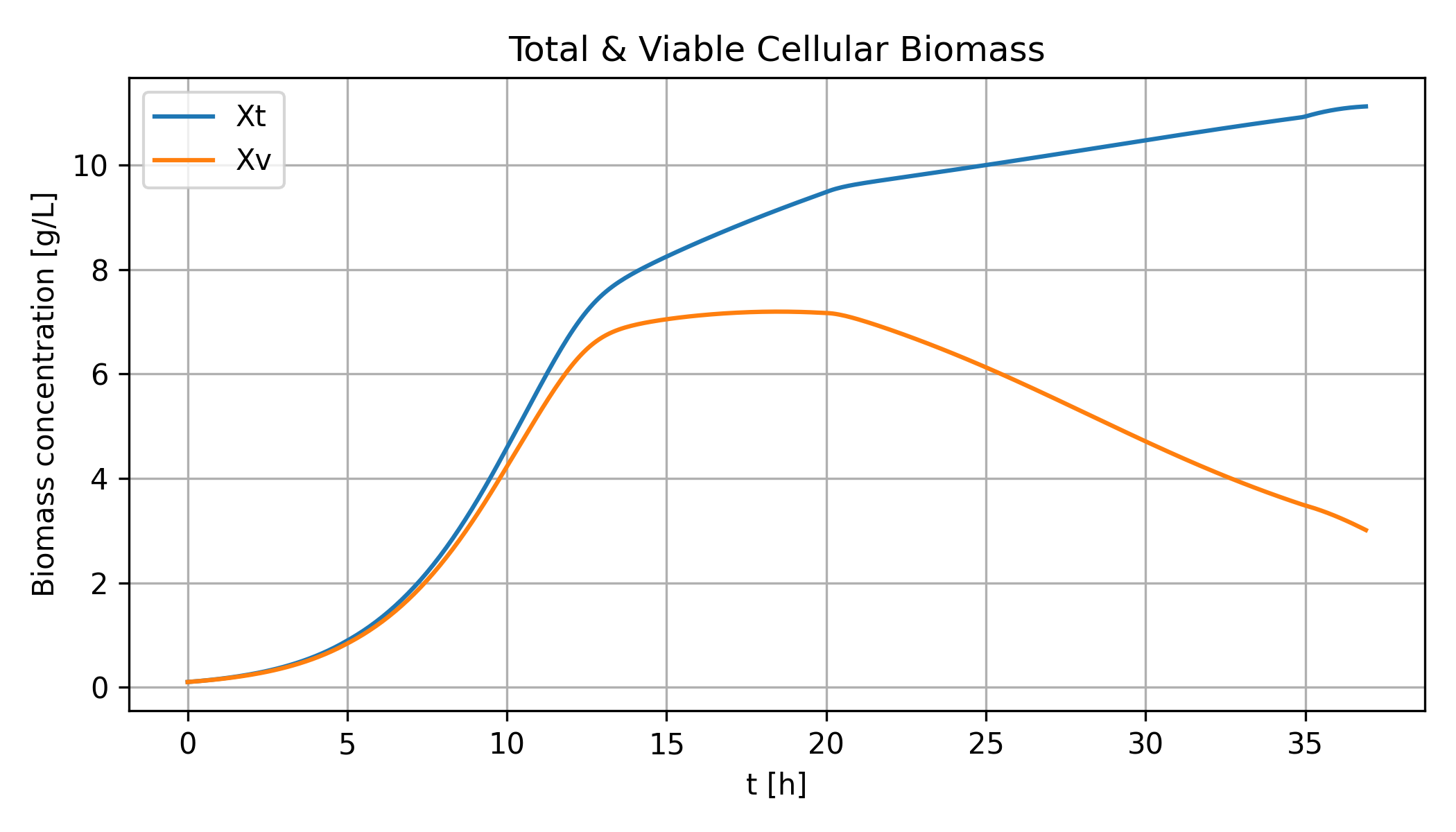
The model simulates biomass, ethanol, and by-product production. The following chart show total biomass and viable (living) biomass in the reactor.

The model can be used to investigate advanced process control to maximize performance subject to a feeding strategy and measured disturbances.

Optimize Ethanol Production

The simulation model of an ethanol bioreactor can be used to optimize the production of ethanol by providing a virtual platform to test different scenarios and strategies without the need for costly and time-consuming experimental trials. Follow these steps to optimize the ethanol production:

1. Define the parameters: Once the model is built, the next step is to define the parameters that affect the production of ethanol. These may include variables such as temperature, substrate concentration, batch time, and other relevant variables.
2. Run simulations: Using the defined parameters, run simulations to determine the best conditions for maximizing ethanol production. The simulations can be run repeatedly, each time changing one or more variables to determine the optimal combination.
3. Analyze the results: After running the simulations, analyze the results to identify the optimal conditions for maximizing ethanol production. The analysis can be done using statistical techniques or data visualization tools to help identify trends and patterns.
4. Optimize the bioreactor: Based on the results of the analysis, optimize the bioreactor operation by adjusting the parameters to the identified optimal conditions. This may involve adjusting the reactor temperature, substrate concentration, or other variables.
5. Validate the model: test the simulation model by comparing the results obtained from the simulation with experimental data obtained from the actual bioreactor. This ensures that the results of the optimization are accurate.

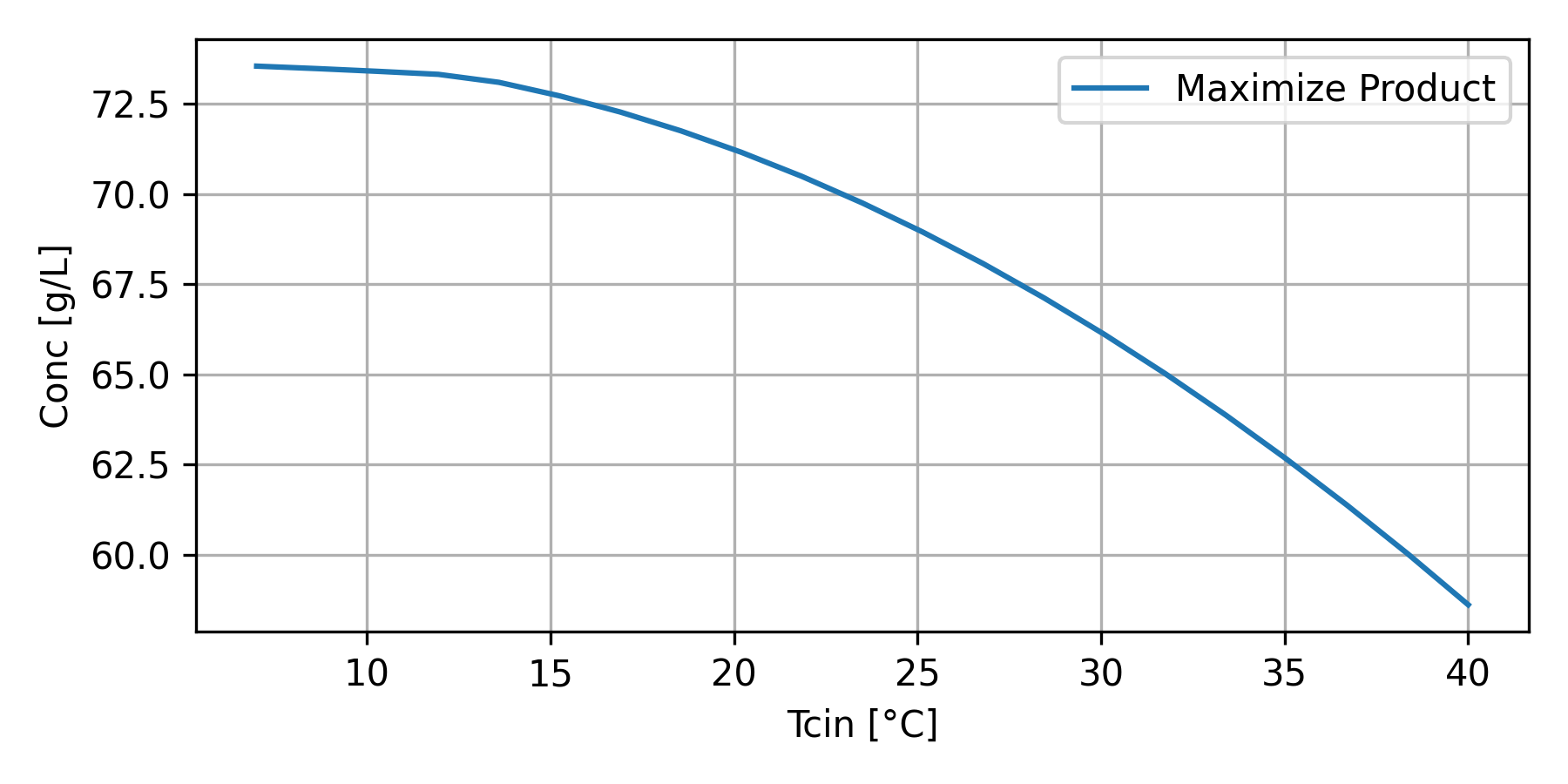
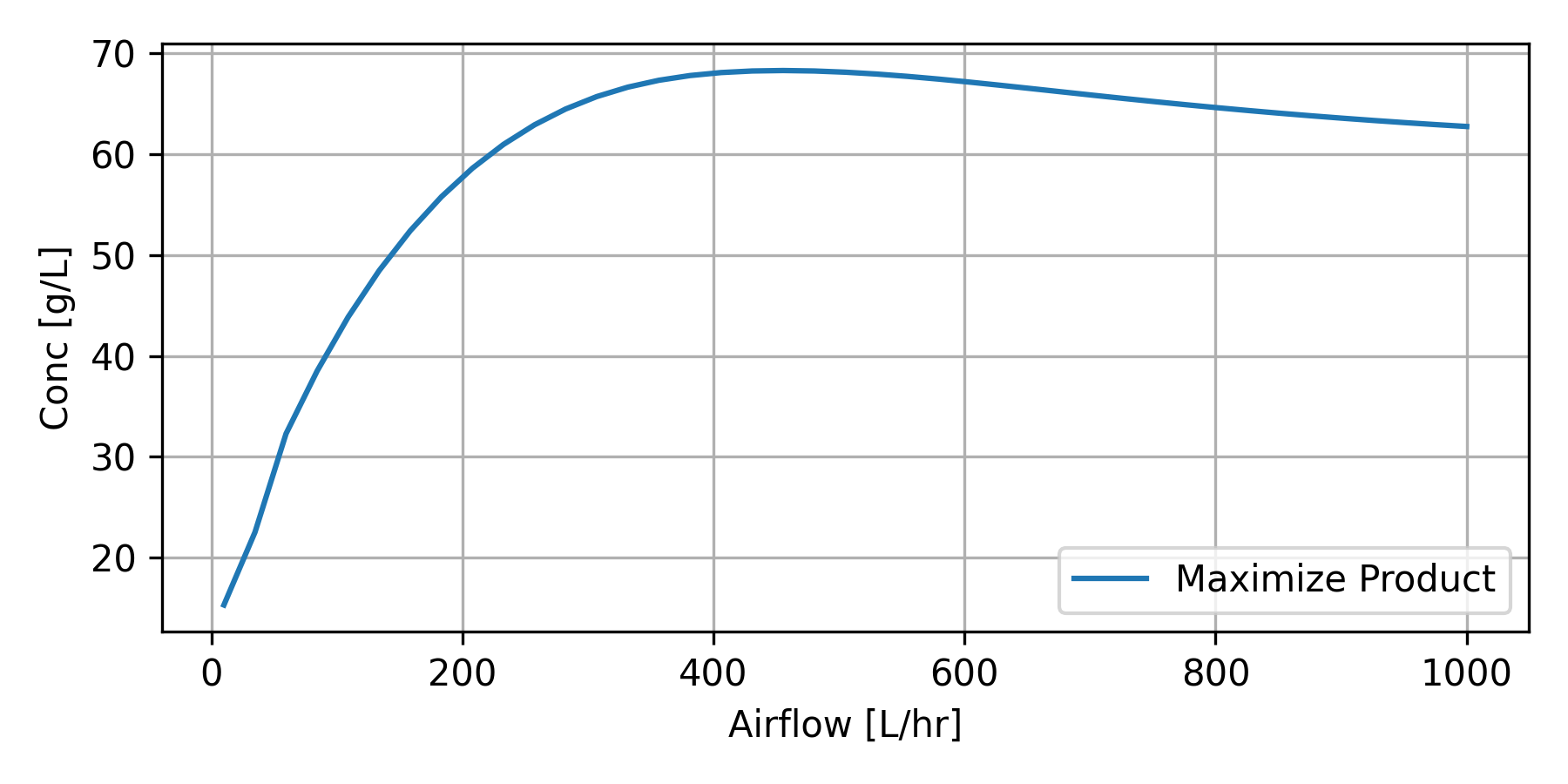
The optimization strategy is used to determine the optimal Tcin (temperature to the cooling jacket) and Fair (air flow).

Maximize Ethanol Production with Cooling Temperature

Temperature control is crucial for maximizing ethanol production, as it directly affects yeast activity and fermentation efficiency. Most ethanol-producing yeasts thrive within an optimal temperature range, typically 30–35°C, where metabolic activity and ethanol yield are maximized. Deviation from this range can slow fermentation or cause thermal stress, reducing cell viability and ethanol production. Bioreactors often use temperature-regulating systems, such as water jackets, heat exchangers, or cooling coils, to maintain the ideal temperature. In large-scale operations, active cooling is essential to counteract heat generated during fermentation. Precise temperature control also helps minimize the production of unwanted by-products and supports consistent ethanol yields. Automated systems with temperature sensors and feedback controls are frequently employed to ensure stable conditions throughout the process.

Maximize Ethanol Production with Air Flow Rate

Ethanol bioreactors can strategically use air to optimize production by supporting yeast health and process efficiency. During initial stages, oxygen is introduced to promote yeast propagation, enhancing cell growth and the production of sterols and fatty acids essential for robust fermentation. Some systems maintain microaerophilic conditions, carefully controlling oxygen levels to balance yeast growth and ethanol synthesis, as excessive oxygen shifts metabolism toward biomass production rather than ethanol. In certain setups, aerobic bacteria are co-cultured with yeast to degrade inhibitors like furfural or acetic acid, improving overall efficiency. Aeration is also used to manage heat and CO₂ accumulation in large-scale systems, though excessive oxygen must be avoided to preserve yields. While fermentation is primarily anaerobic, these controlled applications of air can enhance production by optimizing the fermentation environment.

References

• Bioreactor Simulation for Ethanol Production using GEKKO, Stack Overflow, Nov 9, 2022.