Dynamic Estimation Tuning

Dynamic estimation tuning is the process of adjusting certain objective function terms to give more desirable solutions. As an example, a dynamic estimation application such as moving horizon estimation (MHE) may either track noisy data too closely or the updates may be too slow to catch unmeasured disturbances of interest. Tuning is the process of achieving acceptable estimator performance based on unique aspects of the application.

Common Tuning Parameters for MHE

Tuning typically involves adjustment of objective function terms or constraints that limit the rate of change (DMAX), penalize the rate of change (DCOST), or set absolute bounds (LOWER and UPPER). Measurement availability is indicated by the parameter (FSTATUS). The optimizer can also include (1=on) or exclude (0=off) a certain adjustable parameter (FV) or manipulated variable (MV) with STATUS. Another important tuning consideration is the time horizon length. Including more points in the time horizon allows the estimator to reconcile the model to more data but also increases computational time.

Download MHE Tuning IPython Widget or view on GitHub

Below are common application, FV, MV, and CV tuning constants that are adjusted to achieve desired model predictive control performance.

There are several ways to change the tuning values. Tuning values can either be specified before an application is initialized or while an application is running. To change a tuning value before the application is loaded, use the apm_option() function such as the following example to change the lower bound in MATLAB or Python for the FV named p. 

 apm_option(server,app,'p.LOWER',0)

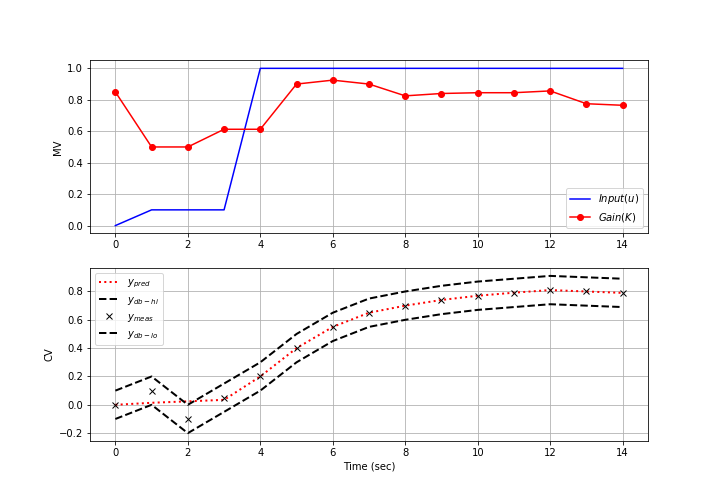
The upper and lower measurement deadband for a CV named y are set to values around the measurement. In this case, an acceptable range for the model prediction is to intersect the measurement of 10.0 between 9.5 and 10.5 with a MEAS_GAP of 1.0 (or +/-0.5). 

 apm_option(server,app,'y.MEAS_GAP',1.0)

Application constants are modified by indicating that the constant belongs to the group apm. IMODE is adjusted to either solve the MHE problem with a simultaneous (5) or sequential (8) method. In the case below, the application IMODE is changed to simultaneous mode. 

 apm_option(server,app,'apm.IMODE',5)

Exercise

Objective: Design an estimator to predict an unknown parameters so that a simple model is able to predict the response of a more complex process. Tune the estimator to achieve either tracking or predictive performance. Estimated time: 1 hour.

Estimator Tuning Source Files

import numpy as np
from random import random
from gekko import GEKKO
import matplotlib.pyplot as plt

n = 1 # process model order

#%% Process
rmt = False
p = GEKKO(remote=rmt)
p.time = [0,.5]

#Parameters
p.u = p.MV(value=0)
p.K = p.Param(value=1) #gain
p.tau = p.Param(value=5) #time constant

#Intermediate
p.x = [p.Intermediate(p.u)]

#Variables
p.x.extend([p.Var() for _ in range(n)])  #state variables
p.y = p.SV() #measurement

#Equations
p.Equations([p.tau/n * p.x[i+1].dt() == -p.x[i+1] + p.x[i] for i in range(n)])
p.Equation(p.y == p.K * p.x[n])

#options
p.options.IMODE = 4

#%% Model
m = GEKKO(remote=rmt)
#0-20 by 0.5 -- discretization must match simulation
m.time = np.linspace(0,20,41)

#Parameters
m.u = m.MV() #input
m.K = m.FV(value=1, lb=0.3, ub=3) #gain
m.tau = m.FV(value=5, lb=1, ub=10) #time constant

#Variables
m.x = m.SV() #state variable
m.y = m.CV() #measurement

#Equations
m.Equations([m.tau * m.x.dt() == -m.x + m.u,
             m.y == m.K * m.x])

#Options
m.options.IMODE = 5 #MHE
m.options.EV_TYPE = 1

# STATUS = 0, optimizer doesn't adjust value
# STATUS = 1, optimizer can adjust
m.u.STATUS = 0
m.K.STATUS = 1
m.tau.STATUS = 1

# FSTATUS = 0, no measurement
# FSTATUS = 1, measurement used to update model
m.u.FSTATUS = 1
m.K.FSTATUS = 0
m.tau.FSTATUS = 0
m.y.FSTATUS = 1

# DMAX = maximum movement each cycle
m.K.DMAX = 1
m.tau.DMAX = .1

# MEAS_GAP = dead-band for measurement / model mismatch
m.y.MEAS_GAP = 0.0

#%% problem configuration
# number of cycles
cycles = 50
# time vector
tm = np.linspace(0,25,51)
# noise level
noise = 0.25

# values of u change randomly over time every 10th step
u_meas = np.zeros(cycles)
step_u = 0
for i in range(0,cycles):
    if ((i-1)%10) == 0:
        # random step (-5 to 5)
        step_u = step_u + (random()-0.5)*10
    u_meas[i] = step_u

#%% run process and estimator for cycles
y_meas = np.zeros(cycles)
y_est = np.zeros(cycles)
k_est = np.zeros(cycles)*np.nan
tau_est = np.zeros(cycles)*np.nan
for i in range(cycles-1):
    # process simulator
    p.u.MEAS = u_meas[i]
    p.solve()
    r = (random()-0.5)*noise
    y_meas[i] = p.y.value[1] + r # add noise

    # estimator
    m.u.MEAS = u_meas[i]
    m.y.MEAS = y_meas[i]
    m.solve()
    y_est[i] = m.y.MODEL
    k_est[i] = m.K.NEWVAL
    tau_est[i] = m.tau.NEWVAL

    plt.clf()
    plt.subplot(4,1,1)
    plt.plot(tm[0:i+1],y_meas[0:i+1],'b-')
    plt.plot(tm[0:i+1],y_est[0:i+1],'r--')
    plt.legend(('meas','pred'))
    plt.ylabel('y')
    plt.subplot(4,1,2)
    plt.plot(tm[0:i+1],np.ones(i+1)*p.K.value[0],'b-')
    plt.plot(tm[0:i+1],k_est[0:i+1],'r--')
    plt.legend(('actual','pred'))
    plt.ylabel('k')
    plt.subplot(4,1,3)
    plt.plot(tm[0:i+1],np.ones(i+1)*p.tau.value[0],'b-')
    plt.plot(tm[0:i+1],tau_est[0:i+1],'r--')
    plt.legend(('actual','pred'))
    plt.ylabel('tau')
    plt.subplot(4,1,4)
    plt.plot(tm[0:i+1],u_meas[0:i+1],'b-')
    plt.legend('u')
    plt.draw()
    plt.pause(0.05)
[$[Get Code]]

Design an estimator to predict K and tau of a 1st order model to predict the dynamic response of a 1st order, 2nd order, and 10th order process. For the 2nd and 10th order systems, there is process/model mismatch. This means that the structure of the model can never exactly match the actual process because the equations are inherently incorrect. The parameter values are adjusted to best approximate the process even though the model is deficient. The process order is adjusted in the file process.apm file in the Constants section. 

 Constants
   ! process model order
   n = 1  ! change to 1, 2, and 10

In each case, tune the estimator to favor either acceptable tracking or predictive performance. Tracking performance is the ability of the estimator to synchronize with measurements and is demonstrated with overall agreement between the model predictions and the measurements. Predictive performance sacrifices tracking performance to achieve more consistent values that are valid over a longer predictive horizon for model predictive control.

Solution

Jupyter Notebook Tip

For Jupyter notebooks, add the following code to allow real-time plots to display instead of creating a new plot for every frame. Use the clear_output() function in the loop where the plot is displayed.

from IPython import display

display.clear_output(wait=True)
[$[Get Code]]

Here is a complete example:

import numpy as np
import matplotlib.pyplot as plt
from IPython import display

x = np.linspace(0, 6 * np.pi, 100)
cos_values = []
sin_values = []
for i in range(len(x)):
    # add the sin and cos of x at index i to the lists
    cos_values.append(np.cos(x[i]))
    sin_values.append(np.sin(x[i]))

    # graph up until index i
    plt.plot(x[:i], cos_values[:i], label='Cos')
    plt.plot(x[:i], sin_values[:i], label='Sin')
    plt.xlabel('input')
    plt.ylabel('output')

    # lines that help with animation
    display.clear_output(wait=True)  # replace figure
    plt.pause(.01)  # wait between figures
[$[Get Code]]
Home | Dynamic Estimation Tuning