Optimal Control Benchmark Problems
Main.DynamicOptimizationBenchmarks History
Hide minor edits - Show changes to markup
 DynOpt Benchmarks (Jupyter Notebook) on GitHub or on Google Colab.
DynOpt Benchmarks (Jupyter Notebook) on GitHub or on Google Colab. DynOpt Benchmarks on GitHub or on Google Colab.
DynOpt Benchmarks on GitHub or on Google Colab. DynOpt Benchmark Solutions on GitHub or on Google Colab.
DynOpt Benchmark Solutions on GitHub or on Google Colab.plt.plot(m.time,x1.value,'k:',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2.value,'b-',LineWidth=2,label=r'$x_2$') plt.plot(m.time,u.value,'r--',LineWidth=2,label=r'$u$')
plt.plot(m.time,x1.value,'k:',lw=2,label=r'$x_1$') plt.plot(m.time,x2.value,'b-',lw=2,label=r'$x_2$') plt.plot(m.time,u.value,'r--',lw=2,label=r'$u$')
plt.plot(m.time,x1.value,'k:',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2.value,'b-',LineWidth=2,label=r'$x_2$') plt.plot(m.time,u.value,'r--',LineWidth=2,label=r'$u$')
plt.plot(m.time,x1.value,'k:',lw=2,label=r'$x_1$') plt.plot(m.time,x2.value,'b-',lw=2,label=r'$x_2$') plt.plot(m.time,u.value,'r--',lw=2,label=r'$u$')
plt.plot(m.time,u,'r-',LineWidth=2,label=r'$u$')
plt.plot(m.time,u,'r-',lw=2,label=r'$u$')
plt.plot(m.time,x1.value,'r--',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2.value,'g:',LineWidth=2,label=r'$x_2$') plt.plot(m.time,x3.value,'k-',LineWidth=2,label=r'$x_3$') plt.plot(m.time,x4.value,'b-',LineWidth=2,label=r'$x_4$')
plt.plot(m.time,x1.value,'r--',lw=2,label=r'$x_1$') plt.plot(m.time,x2.value,'g:',lw=2,label=r'$x_2$') plt.plot(m.time,x3.value,'k-',lw=2,label=r'$x_3$') plt.plot(m.time,x4.value,'b-',lw=2,label=r'$x_4$')
plt.plot(m.time,x1.value,'k:',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2.value,'b-',LineWidth=2,label=r'$x_2$') plt.plot(m.time,u.value,'r--',LineWidth=2,label=r'$u$')
plt.plot(m.time,x1.value,'k:',lw=2,label=r'$x_1$') plt.plot(m.time,x2.value,'b-',lw=2,label=r'$x_2$') plt.plot(m.time,u.value,'r--',lw=2,label=r'$u$')
plt.plot(m.time,x1.value,'k:',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2.value,'b-',LineWidth=2,label=r'$x_2$')
plt.plot(m.time,x1.value,'k:',lw=2,label=r'$x_1$') plt.plot(m.time,x2.value,'b-',lw=2,label=r'$x_2$')
plt.plot(m.time,T.value,'r--',LineWidth=2,label=r'$T$')
plt.plot(m.time,T.value,'r--',lw=2,label=r'$T$')
plt.plot(m.time,x1.value,'k:',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2.value,'b-',LineWidth=2,label=r'$x_2$')
plt.plot(m.time,x1.value,'k:',lw=2,label=r'$x_1$') plt.plot(m.time,x2.value,'b-',lw=2,label=r'$x_2$')
plt.plot(m.time,u.value,'r-',LineWidth=2,label=r'$u$')
plt.plot(m.time,u.value,'r-',lw=2,label=r'$u$')
(:title Optimal Control Problems:)
(:title Optimal Control Benchmark Problems:)
 Dynamic Optimization Benchmarks (Jupyter Notebook) on GitHub or on Google Colab.
Dynamic Optimization Benchmarks (Jupyter Notebook) on GitHub or on Google Colab. DynOpt Benchmarks (Jupyter Notebook) on GitHub or on Google Colab.
DynOpt Benchmarks (Jupyter Notebook) on GitHub or on Google Colab. Dynamic Optimization Benchmarks on GitHub or on Google Colab.
Dynamic Optimization Benchmarks on GitHub or on Google Colab. Dynamic Optimization Benchmarks (Jupyter Notebook) on GitHub or on Google Colab.
Dynamic Optimization Benchmarks (Jupyter Notebook) on GitHub or on Google Colab.Objective: Solve the dynamic optimization benchmark problems2 and MoreDynamicOptimizationBenchmarks. For each problem, create a program to optimize and display the results. Estimated Time (each): 30 minutes
Objective: Solve the dynamic optimization benchmark problems2 and more dynamic optimization benchmark problems. Complete the 9 exercises as shown in the Jupyter Notebook link below. For each problem, create a program to optimize and display the results. Estimated Time (each): 10-30 minutes
Objective: Set up and solve three of the five dynamic optimization benchmark problems2. Create a program to optimize and display the results. Estimated Time (each): 30 minutes
Objective: Solve the dynamic optimization benchmark problems2 and MoreDynamicOptimizationBenchmarks. For each problem, create a program to optimize and display the results. Estimated Time (each): 30 minutes
 Dynamic Optimization Benchmarks on GitHub or on Google Colab.
Dynamic Optimization Benchmarks on GitHub or on Google Colab.$$\frac{dx_4}{dt}=x_1^2+x_2^2+0.0005 \left(x_2 + 16 \, t -8 -0.1x_3\,u^2\right)^2$$
$$\frac{dx_4}{dt}=x_1^2+x_2^2+0.005 \left(x_2 + 16 \, t -8 -0.1x_3\,u^2\right)^2$$
(:title Optimal Control Problems:) (:keywords nonlinear control, optimal control, dynamic optimization, engineering optimization, MATLAB, Python, GEKKO, differential, algebraic, modeling language, university course:) (:description Optimal control problems solved with Dynamic Optimization in MATLAB, Excel, and Python.:)
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/r42PEsh5Nxg" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> (:htmlend:)
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/gptRJ5x7Ybs" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> (:htmlend:)
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/mdefRrGarP0" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> (:htmlend:)
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/mdefRrGarP0" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> (:htmlend:)
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/mdefRrGarP0" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> (:htmlend:)
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/mdefRrGarP0" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> (:htmlend:)
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/mdefRrGarP0" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> (:htmlend:)
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/dxC__nDnmCY" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> (:htmlend:)
- Show source
import numpy as np import matplotlib.pyplot as plt from gekko import GEKKO
m = GEKKO()
nt = 101 m.time = np.linspace(0,12,nt)
- Parameters
u = m.MV(value=1,ub=1,lb=0) u.STATUS = 1 u.DCOST = 0
- Variables
x1 = m.Var(value=1) x2 = m.Var(value=0)
p = np.zeros(nt) p[-1] = 1.0 final = m.Param(value=p)
- Equations
m.Equation(x1.dt()==u*(10*x2-x1)) m.Equation(x2.dt()==-u*(10*x2-x1)-(1-u)*x2)
- Objective Function
m.Obj(-final*(1-x1-x2))
m.options.IMODE = 6 m.solve()
print('Objective: ' + str(1-x1[-1]-x2[-1]))
plt.figure(1)
plt.subplot(2,1,1) plt.plot(m.time,x1.value,'k:',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2.value,'b-',LineWidth=2,label=r'$x_2$') plt.ylabel('Value') plt.legend(loc='best')
plt.subplot(2,1,2) plt.plot(m.time,u.value,'r-',LineWidth=2,label=r'$u$') plt.legend(loc='best') plt.xlabel('Time') plt.ylabel('Value')
plt.show()
- Show source
import numpy as np import matplotlib.pyplot as plt from gekko import GEKKO
m = GEKKO()
nt = 101 m.time = np.linspace(0,1,nt)
- Parameters
T = m.MV(value=362,ub=398,lb=298) T.STATUS = 1 T.DCOST = 0
- Variables
x1 = m.Var(value=1) x2 = m.Var(value=0)
p = np.zeros(nt) p[-1] = 1.0 final = m.Param(value=p)
- Intermediates
k1 = m.Intermediate(4000*m.exp(-2500/T)) k2 = m.Intermediate(6.2e5*m.exp(-5000/T))
- Equations
m.Equation(x1.dt()==-k1*x1**2) m.Equation(x2.dt()==k1*x1**2 - k2*x2)
- Objective Function
m.Obj(-x2*final)
m.options.IMODE = 6 m.solve()
print('Objective: ' + str(x2[-1]))
plt.figure(1)
plt.subplot(2,1,1) plt.plot(m.time,x1.value,'k:',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2.value,'b-',LineWidth=2,label=r'$x_2$') plt.ylabel('Value') plt.legend(loc='best')
plt.subplot(2,1,2) plt.plot(m.time,T.value,'r--',LineWidth=2,label=r'$T$') plt.legend(loc='best') plt.xlabel('Time') plt.ylabel('Value')
plt.show()
- Show source
import numpy as np import matplotlib.pyplot as plt from gekko import GEKKO
m = GEKKO()
nt = 101 m.time = np.linspace(0,1,nt)
- Parameters
u = m.MV(value=1,ub=5,lb=0) u.STATUS = 1
- Variables
x1 = m.Var(value=1) x2 = m.Var(value=0)
p = np.zeros(nt) p[-1] = 1.0 final = m.Param(value=p)
- Equations
m.Equation(x1.dt()==-(u+0.5*u**2)*x1) m.Equation(x2.dt()==u*x1)
- Objective Function
m.Obj(-x2*final)
m.options.IMODE = 6 m.solve()
print('Objective: ' + str(x2[-1]))
plt.figure(1) plt.plot(m.time,x1.value,'k:',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2.value,'b-',LineWidth=2,label=r'$x_2$') plt.plot(m.time,u.value,'r--',LineWidth=2,label=r'$u$') plt.legend(loc='best') plt.xlabel('Time') plt.ylabel('Value') plt.show()
$$\min_{T(t)} x_2 \left( t_f \right)$$
$$\max_{T(t)} x_2 \left( t_f \right)$$
$$\min_{u(t)} x_2 \left( t_f \right)$$
$$\max_{u(t)} x_2 \left( t_f \right)$$
plt.plot(m.time,x1,'k:',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2,'b-',LineWidth=2,label=r'$x_2$') plt.plot(m.time,u,'r--',LineWidth=2,label=r'$u$')
plt.plot(m.time,x1.value,'k:',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2.value,'b-',LineWidth=2,label=r'$x_2$') plt.plot(m.time,u.value,'r--',LineWidth=2,label=r'$u$')
plt.plot(m.time,x1,'k:',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2,'b-',LineWidth=2,label=r'$x_2$') plt.plot(m.time,u,'r--',LineWidth=2,label=r'$u$')
plt.plot(m.time,x1.value,'k:',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2.value,'b-',LineWidth=2,label=r'$x_2$') plt.plot(m.time,u.value,'r--',LineWidth=2,label=r'$u$')
plt.plot(m.time,x1,'r--',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2,'g:',LineWidth=2,label=r'$x_2$') plt.plot(m.time,x3,'k-',LineWidth=2,label=r'$x_3$') plt.plot(m.time,x4,'b-',LineWidth=2,label=r'$x_4$')
plt.plot(m.time,x1.value,'r--',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2.value,'g:',LineWidth=2,label=r'$x_2$') plt.plot(m.time,x3.value,'k-',LineWidth=2,label=r'$x_3$') plt.plot(m.time,x4.value,'b-',LineWidth=2,label=r'$x_4$')
(:toggle hide solution1 button show="Show Solutions for Problem 1a and 1b":) (:div id=solution1:)
(:divend:)
Solution to Benchmarks 1a and 1b
Solutions to Benchmarks 1a and 1b
(:toggle hide solution1 button show="Show Solutions for Problem 1a and 1b":) (:div id=solution1:)
(:divend:)
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/WHnIfKUfjQY" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> (:htmlend:)
$$\min_{u(t)} 1 - x_1 \left( t_f \right) - x_2 \left( t_f \right)$$
$$\max_{u(t)} \left(1 - x_1 \left( t_f \right) - x_2 \left( t_f \right) \right)$$
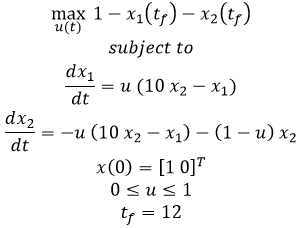
$$\min_{u(t)} 1 - x_1 \left( t_f \right) - x_2 \left( t_f \right)$$ $$\mathrm{subject \; to}$$ $$\frac{dx_1}{dt}=u \left(10 \, x_2 - x_1 \right)$$ $$\frac{dx_2}{dt}=-u \left(10 \, x_2 - x_1 \right)-\left(1-u\right) x_2$$ $$x(0) = [1 \; 0]^T$$ $$0 \le u \le 1$$ $$t_f=12$$
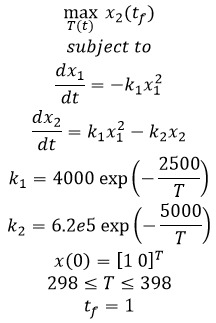
$$\min_{T(t)} x_2 \left( t_f \right)$$ $$\mathrm{subject \; to}$$ $$\frac{dx_1}{dt}=-k_1 \, x_1^2$$ $$\frac{dx_2}{dt}=k_1 \, x_1^2 - k_2 \, x_2$$ $$k_1 = 4000 \, \exp{\left(-\frac{2500}{T}\right)}$$ $$k_2 = 6.2e5 \, \exp{\left(-\frac{5000}{T}\right)}$$ $$x(0) = [1 \; 0]^T$$ $$298 \le T \le 398$$ $$t_f=1$$
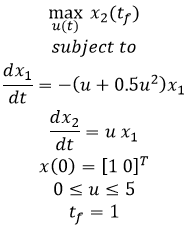
$$\min_{u(t)} x_2 \left( t_f \right)$$ $$\mathrm{subject \; to}$$ $$\frac{dx_1}{dt}=-\left(u+0.5u^2\right) x_1$$ $$\frac{dx_2}{dt}=u \, x_1$$ $$x(0) = [1 \; 0]^T$$ $$0 \le u \le 5$$ $$t_f=1$$
- Show source
import numpy as np import matplotlib.pyplot as plt from gekko import GEKKO
m = GEKKO()
nt = 101 m.time = np.linspace(0,1,nt)
- Parameters
u = m.MV(value=9,lb=-4,ub=10) u.STATUS = 1 u.DCOST = 0
- Variables
t = m.Var(value=0) x1 = m.Var(value=0) x2 = m.Var(value=-1) x3 = m.Var(value=-np.sqrt(5)) x4 = m.Var(value=0)
p = np.zeros(nt) p[-1] = 1.0 final = m.Param(value=p)
- Equations
m.Equation(t.dt()==1) m.Equation(x1.dt()==x2) m.Equation(x2.dt()==-x3*u+16*t-8) m.Equation(x3.dt()==u) m.Equation(x4.dt()==x1**2+x2**2 +0.005*(x2+16*t-8-0.1*x3*(u**2))**2)
- Objective Function
m.Obj(x4*final)
m.options.IMODE = 6 m.options.NODES = 4 m.options.MV_TYPE = 1 m.options.SOLVER = 3 m.solve()
print(m.path)
print('Objective = min x4(tf): ' + str(x4[-1]))
plt.figure(1) plt.subplot(2,1,1) plt.plot(m.time,u,'r-',LineWidth=2,label=r'$u$') plt.legend(loc='best') plt.subplot(2,1,2) plt.plot(m.time,x1,'r--',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2,'g:',LineWidth=2,label=r'$x_2$') plt.plot(m.time,x3,'k-',LineWidth=2,label=r'$x_3$') plt.plot(m.time,x4,'b-',LineWidth=2,label=r'$x_4$') plt.legend(loc='best') plt.xlabel('Time') plt.ylabel('Value') plt.show()
nt = 501
nt = 101
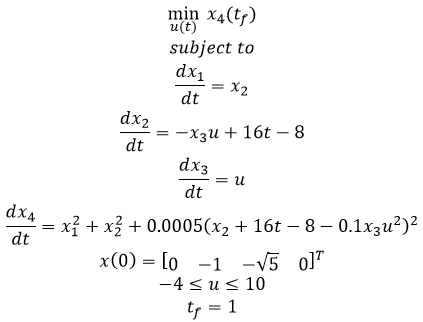
$$\min_{u(t)} x_4 \left( t_f \right)$$ $$\mathrm{subject \; to}$$ $$\frac{dx_1}{dt}=x_2$$ $$\frac{dx_2}{dt}=-x_3 \, u + 16 \, t - 8$$ $$\frac{dx_3}{dt}=u$$ $$\frac{dx_4}{dt}=x_1^2+x_2^2+0.0005 \left(x_2 + 16 \, t -8 -0.1x_3\,u^2\right)^2$$ $$x(0) = [0 \; -1 \; -\sqrt{5} \; 0]^T$$ $$-4 \le u \le 10$$ $$t_f=1$$
$$x(0) = [1 0]^T$$
$$x(0) = [1 \; 0]^T$$
(:toggle hide gekko1a button show="Show GEKKO (Python) Code":)
Example 1b
- Nonlinear, unconstrained, minimize final state with terminal constraint
$$\min_{u(t)} x_2 \left( t_f \right)$$ $$\mathrm{subject \; to}$$ $$\frac{dx_1}{dt}=u$$ $$\frac{dx_2}{dt}=x_1^2 + u^2$$ $$x(0) = [1 \; 0]^T$$ $$x_1 \left( t_f \right)=1$$ $$t_f=1$$
Solution to Benchmarks 1a and 1b
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/mmCFF3-6sGg" frameborder="0" allowfullscreen></iframe> (:htmlend:)
(:toggle hide gekko1a button show="Show GEKKO (Python) Code for 1a":)
Example 1b
- Nonlinear, unconstrained, minimize final state with terminal constraint
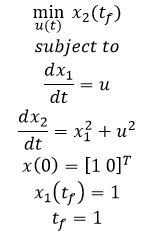
Solution to Benchmarks 1a and 1b
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/mmCFF3-6sGg" frameborder="0" allowfullscreen></iframe> (:htmlend:)
(:toggle hide gekko1b button show="Show GEKKO (Python) Code for 1b":) (:div id=gekko1b:) (:source lang=python:) import numpy as np import matplotlib.pyplot as plt from gekko import GEKKO
m = GEKKO()
nt = 101 m.time = np.linspace(0,1,nt)
- Variables
x1 = m.Var(value=1) x2 = m.Var(value=0) u = m.Var(value=-0.48)
p = np.zeros(nt) p[-1] = 1.0 final = m.Param(value=p)
- Equations
m.Equation(x1.dt()==u) m.Equation(x2.dt()==x1**2 + u**2) m.Equation(final*(x1-1)==0)
- Objective Function
m.Obj(x2*final)
m.options.IMODE = 6 m.solve()
plt.figure(1) plt.plot(m.time,x1,'k:',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2,'b-',LineWidth=2,label=r'$x_2$') plt.plot(m.time,u,'r--',LineWidth=2,label=r'$u$') plt.legend(loc='best') plt.xlabel('Time') plt.ylabel('Value') plt.show() (:sourceend:) (:divend:)
(:toggle hide gekko2 button show="Show GEKKO (Python) Code":) (:div id=gekko2:) (:source lang=python:)
- Show source
(:sourceend:) (:divend:)
(:toggle hide gekko3 button show="Show GEKKO (Python) Code":) (:div id=gekko3:) (:source lang=python:)
- Show source
(:sourceend:) (:divend:)
(:toggle hide gekko4 button show="Show GEKKO (Python) Code":) (:div id=gekko4:) (:source lang=python:)
- Show source
(:sourceend:) (:divend:)
(:toggle hide gekko5 button show="Show GEKKO (Python) Code":) (:div id=gekko5:) (:source lang=python:)
- Show source
(:sourceend:) (:divend:)
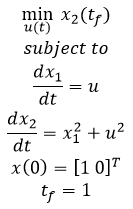
$$\min_{u(t)} x_2 \left( t_f \right)$$ $$\mathrm{subject \; to}$$ $$\frac{dx_1}{dt}=u$$ $$\frac{dx_2}{dt}=x_1^2 + u^2$$ $$x(0) = [1 0]^T$$ $$t_f=1$$
Objective: Set up and solve five dynamic optimization benchmark problems2. Create a program to optimize and display the results. Estimated Time (each): 30 minutes
Objective: Set up and solve three of the five dynamic optimization benchmark problems2. Create a program to optimize and display the results. Estimated Time (each): 30 minutes
(:toggle hide gekko1a button show="Show GEKKO (Python) Code":) (:div id=gekko1a:) (:source lang=python:) import numpy as np import matplotlib.pyplot as plt from gekko import GEKKO
m = GEKKO()
nt = 501 m.time = np.linspace(0,1,nt)
- Variables
x1 = m.Var(value=1) x2 = m.Var(value=0) u = m.Var(value=-0.75)
p = np.zeros(nt) p[-1] = 1.0 final = m.Param(value=p)
- Equations
m.Equation(x1.dt()==u) m.Equation(x2.dt()==x1**2 + u**2)
- Objective Function
m.Obj(x2*final)
m.options.IMODE = 6 m.solve()
plt.figure(1) plt.plot(m.time,x1,'k:',LineWidth=2,label=r'$x_1$') plt.plot(m.time,x2,'b-',LineWidth=2,label=r'$x_2$') plt.plot(m.time,u,'r--',LineWidth=2,label=r'$u$') plt.legend(loc='best') plt.xlabel('Time') plt.ylabel('Value') plt.show() (:sourceend:) (:divend:)
Objective: Set up and solve several dynamic optimization benchmark problems2. Create a program to optimize and display the results. Estimated Time (each): 30 minutes
Objective: Set up and solve five dynamic optimization benchmark problems2. Create a program to optimize and display the results. Estimated Time (each): 30 minutes
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/YBlOF9ATaHI" frameborder="0" allowfullscreen></iframe> (:htmlend:)
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/yFprG0iJQUE" frameborder="0" allowfullscreen></iframe> (:htmlend:)
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/sYBE3-PVS9g" frameborder="0" allowfullscreen></iframe> (:htmlend:)
- Hedengren, J. D. and Asgharzadeh Shishavan, R., Powell, K.M., and Edgar, T.F., Nonlinear Modeling, Estimation and Predictive Control in APMonitor, Computers and Chemical Engineering, Volume 70, pg. 133–148, 2014. Article
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/JP2rH7IPYvc" frameborder="0" allowfullscreen></iframe> (:htmlend:)
Solution
Solution to Benchmarks 1a and 1b
Solution
Solution to Benchmark 2
Solution
Solution to Benchmark 3
Solution
Solution to Benchmark 4
Solution
Solution to Benchmark 5
- Example 1a - Nonlinear, unconstrained, minimize final state
Example 1a
- Nonlinear, unconstrained, minimize final state
- Example 1b - Nonlinear, unconstrained, minimize final state with terminal constraint
Example 1b
- Nonlinear, unconstrained, minimize final state with terminal constraint
- Example 2 - Nonlinear, constrained, minimize final state
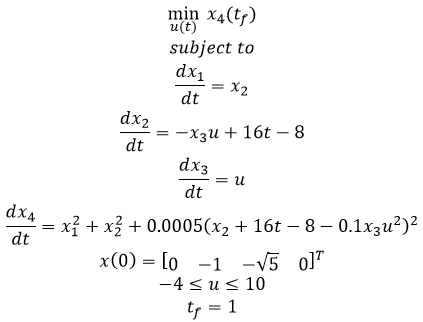
- Example 3 - Tubular reactor with parallel reaction
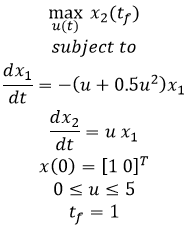
- Example 4 - Batch reactor with consecutive reactions A->B->C
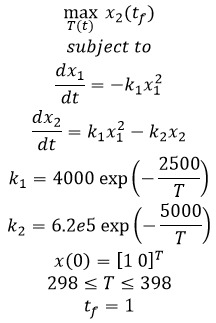
Example 5 - Catalytic reactor with A<->B->C
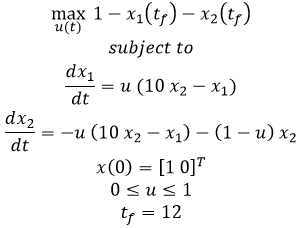
Example 2
- Nonlinear, constrained, minimize final state
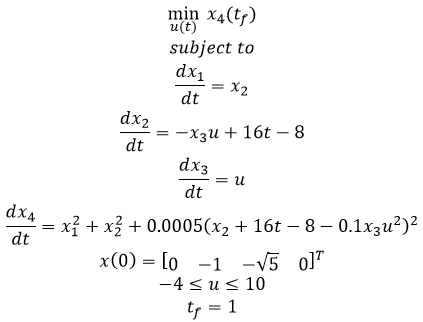
Solution
Example 3
- Tubular reactor with parallel reaction
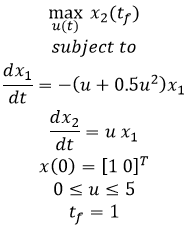
Solution
Example 4
- Batch reactor with consecutive reactions A->B->C
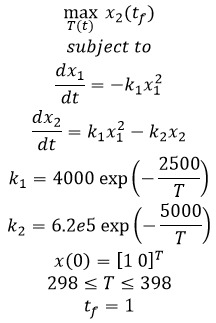
Solution
Example 5
- Catalytic reactor with A<->B->C
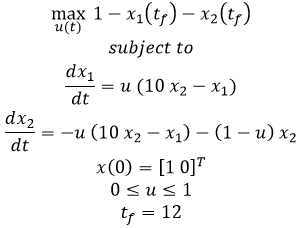
Solution
Exercise
Objective: Set up and solve several dynamic optimization benchmark problems2. Create a program to optimize and display the results. Estimated Time (each): 30 minutes
- Example 1a - Nonlinear, unconstrained, minimize final state
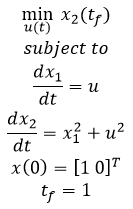
- Example 1b - Nonlinear, unconstrained, minimize final state with terminal constraint
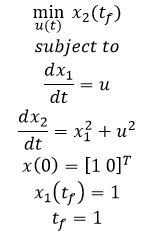
- Example 2 - Nonlinear, constrained, minimize final state
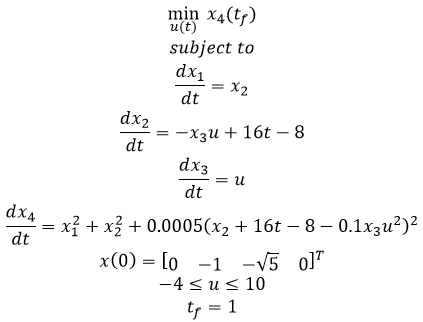
- Example 3 - Tubular reactor with parallel reaction
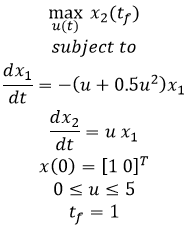
- Example 4 - Batch reactor with consecutive reactions A->B->C
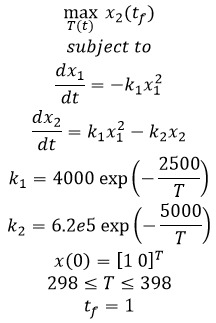
Example 5 - Catalytic reactor with A<->B->C
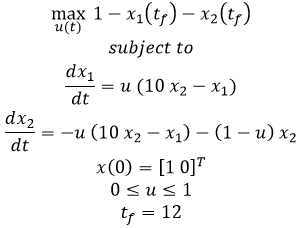
Solution
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/mmCFF3-6sGg" frameborder="0" allowfullscreen></iframe> (:htmlend:)
References
- M. Čižniar, M. Fikar, M.A. Latifi: A MATLAB Package for Dynamic Optimisation of Processes, 7th International Scientific – Technical Conference – Process Control 2006, June 13 – 16, 2006, Kouty nad Desnou, Czech Republic. Article