Dynamic Control Tuning

Dynamic controller tuning is the process of adjusting certain objective function terms to give more desirable solutions. As an example, a dynamic control application may either exhibit too aggressive manipulated variable movement or be too sluggish during set-point changes. Tuning is the iterative process of finding acceptable values that work over a wide range of operating conditions.

MPC Tuning IPython Widget

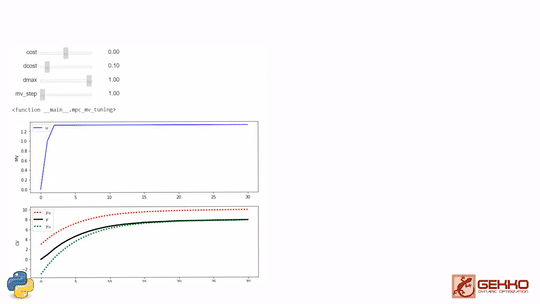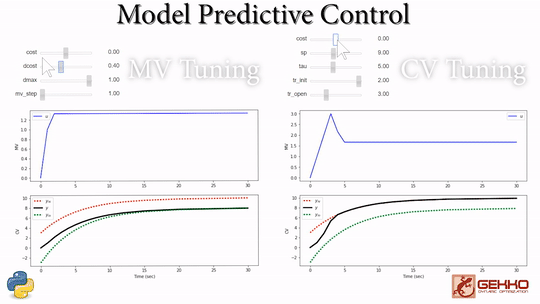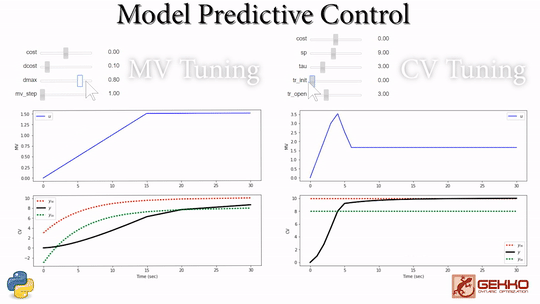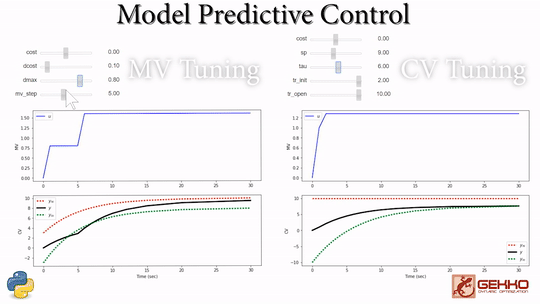
Common Tuning Parameters for MPC

Tuning typically involves adjustment of objective function terms or constraints that limit the rate of change (DMAX), penalize the rate of change (DCOST), or set absolute bounds (LOWER and UPPER). Measurement availability is indicated by the parameter (FSTATUS). The optimizer can also include (1=on) or exclude (0=off) a certain manipulated variable (MV) or controlled variable with STATUS. Below are common application, MV, and CV tuning constants that are adjusted to achieve desired model predictive control performance.

There are several ways to change the tuning values. Tuning values can either be specified before an application is initialized or while an application is running. To change a tuning value before the application is loaded, use the apm_option() function such as the following example to change the lower bound in MATLAB or Python for the MV named u. 

 apm_option(server,app,'u.LOWER',0)

The upper and lower deadband targets for a CV named y are set to values around a desired set point of 10.0. In this case, an acceptable range for this CV is between 9.5 and 10.5. 

 sp = 10.0
 apm_option(server,app,'y.SPHI',sp+0.5)
 apm_option(server,app,'y.SPHI',sp-0.5)

Application constants are modified by indicating that the constant belongs to the group nlc. IMODE is adjusted to either solve the MPC problem with a simultaneous (6) or sequential (9) method. In the case below, the application IMODE is changed to simultaneous mode. 

 apm_option(server,app,'nlc.IMODE',6)

Exercise

Objective: Design a model predictive controller with one manipulated variable and two controlled variables with competing objectives that cannot be simultaneously satisfied. Tune the controller to achieve best performance. Estimated time: 2 hours.

Use the following system of linear differential equations for this exercise by placing the model definition in the file myModel.apm (APMonitor) or in a Python script (Gekko).

APMonitor Model 

 Parameters
  u
 Variables
  x
  y
 Equations
  5 * $x = -x + 1.5 * u
  15 * $y = -y + 3.0 * u

Gekko Model

import numpy as np
from gekko import GEKKO
m = GEKKO()
t = np.linspace(0,15,76)
m.time = t # 0.2 cycle time
u = m.MV(1,name='u')
x = m.CV(name='x')
y = m.CV(name='y')
m.Equations([5*x.dt() ==-x+1.5*u,\
             15*y.dt()==-y+3.0*u])
[$[Get Code]]

In this case, the parameter u is the manipulated variable and x and y are the controlled variables. It is desired to maximize x and maintain values between 9 and 10. It is desired to maintain values of y between 2 and 7. For the first 10 minutes, the priority is to maintain the range for y and following this time period, it is desired to track the range for x. Tune the controller to meet these objectives while minimizing MV movement.

Solution

import numpy as np
from gekko import GEKKO
import matplotlib.pyplot as plt
import json
from IPython import display
from IPython import get_ipython

# detect if IPython is running
ipython = get_ipython() is not None

m = GEKKO(remote=False)
t = np.linspace(0,15,31)
m.time = t # 0.5 cycle time
u = m.MV(1,name='u')
x = m.CV(name='x')
y = m.CV(name='y')
m.Equations([5*x.dt() ==-x+1.5*u,\
             15*y.dt()==-y+3.0*u])
m.options.IMODE = 6
m.options.NODES = 3

# MV tuning
u.DCOST   = 0.1
u.DMAX    = 1.5
u.STATUS  = 1
u.FSTATUS = 0
u.UPPER   = 10
u.LOWER   = 0

# CV tuning
x.STATUS  = 1
x.FSTATUS = 0
x.SPHI    = 10
x.SPLO    = 9
x.TAU     = 2
x.TR_INIT = 1
x.TR_OPEN = 5
x.WSPHI   = 100
x.WSPLO   = 100

y.STATUS  = 1
y.FSTATUS = 0
y.SPHI    = 7
y.SPLO    = 2
y.TAU     = 0
y.TR_INIT = 0
y.TR_OPEN = 1
y.WSPHI   = 200
y.WSPLO   = 50

# Make an MP4 animation?
make_mp4 = True
if make_mp4:
    import imageio  # required to make animation
    import os
    try:
        os.mkdir('./figures')
    except:
        pass

# plot solution
plt.figure(figsize=(8,5))
plt.ion()
plt.show()

for i in range(40):
    m.solve(disp=False)

    # update time
    tm = m.time+i*0.5

    # x is more important at t=10
    if tm[0]>=10:
        x.WSPLO = 500
        x.WSPHI = 500

    # get trajectory information
    with open(m.path+'//results.json') as f:
        z = json.load(f)

    if ipython:
        display.clear_output(wait=True)
    else:
        plt.clf()

    plt.figure(1,figsize=(8,5))
    plt.subplot(3,1,1)
    plt.plot(tm,u.value,'k-',lw=2,label='u')
    plt.ylim([-1,11])
    plt.legend(loc=1)
    plt.ylabel('MV')

    plt.subplot(3,1,2)
    plt.plot(tm,x.value,'b-',lw=2,label='x')
    plt.plot(tm,z['x.tr_hi'],'k--',label='x traj')
    plt.plot(tm,z['x.tr_lo'],'k--')
    plt.legend(loc=1)

    plt.subplot(3,1,3)
    plt.plot(tm,y.value,'r-',lw=2,label='y')
    plt.plot(tm,z['y.tr_hi'],'k--',label='y traj')
    plt.plot(tm,z['y.tr_lo'],'k--')
    plt.legend(loc=1)
    plt.draw()
    if make_mp4:
        filename='./figures/plot_'+str(i+10000)+'.png'
        plt.savefig(filename)
    plt.pause(0.01)

# generate mp4 from png figures
if make_mp4:
    images = []
    for i in range(40):
        filename='./figures/plot_'+str(i+10000)+'.png'
        images.append(imageio.imread(filename))
    try:
        imageio.mimsave('results.mp4', images)
    except:
        print('Error: Install mp4 generator with "pip install imageio-ffmpeg"')
[$[Get Code]]
MPC Tuning Solution (APM MATLAB and APM Python
Home | Dynamic Control Tuning