Advanced Temperature Control
Main.AdvancedTemperatureControl History
Hide minor edits - Show changes to markup
background-color: #0000ff;
background-color: #1e90ff;
width: 300px;
width: 100%;
- TCLab Files on GitHub
- TCLab Solutions on GitHub
- TCLab for Jupyter Notebook
Model Development
Digital Twin Model Development
Parameter and State Estimation
Machine Learning with Parameter and State Estimation
(:html:) <script type="text/javascript"> _linkedin_partner_id = "452500"; window._linkedin_data_partner_ids = window._linkedin_data_partner_ids || []; window._linkedin_data_partner_ids.push(_linkedin_partner_id); </script><script type="text/javascript"> (function(){var s = document.getElementsByTagName("script")[0]; var b = document.createElement("script"); b.type = "text/javascript";b.async = true; b.src = "https://snap.licdn.com/li.lms-analytics/insight.min.js"; s.parentNode.insertBefore(b, s);})(); </script> <noscript> <img height="1" width="1" style="display:none;" alt="" src="https://dc.ads.linkedin.com/collect/?pid=452500&fmt=gif" /> </noscript> (:htmlend:)
Lab Problem Statements
Advanced Control Labs with Solutions
- Lab F - Linear Model Predictive Control
- Lab G - Nonlinear Model Predictive Control
- Lab H - Moving Horizon Estimation with MPC
Data and Solutions
Lab A
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/SomZYxmIDE8" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> (:htmlend:)
- SISO Energy Balance Solution with MATLAB and Python
- Steady state data, 1 heater
- Dynamic data, 1 heater
(:toggle hide gekko_labAd button show="Lab A: Python TCLab Generate Step Data":) (:div id=gekko_labAd:) (:source lang=python:) import numpy as np import pandas as pd import tclab import time import matplotlib.pyplot as plt
- generate step test data on Arduino
filename = 'tclab_dyn_data1.csv'
- heater steps
Qd = np.zeros(601) Qd[10:200] = 80 Qd[200:400] = 20 Qd[400:] = 50
- Connect to Arduino
a = tclab.TCLab() fid = open(filename,'w') fid.write('Time,H1,T1\n') fid.close()
- run step test (10 min)
for i in range(601):
# set heater value
a.Q1(Qd[i])
print('Time: ' + str(i) + ' H1: ' + str(Qd[i]) + ' T1: ' + str(a.T1))
# wait 1 second
time.sleep(1)
# write results to file
fid = open(filename,'a')
fid.write(str(i)+',str(Qd[i]),str(a.T1)\n')
fid.close()
- close connection to Arduino
a.close()
- read data file
data = pd.read_csv(filename)
- plot measurements
plt.figure() plt.subplot(2,1,1) plt.plot(data['Time'],data['H1'],'b-',label='Heater 1') plt.ylabel('Heater (%)') plt.legend(loc='best') plt.subplot(2,1,2) plt.plot(data['Time'],data['T1'],'r.',label='Temperature 1') plt.ylabel('Temperature (degC)') plt.legend(loc='best') plt.xlabel('Time (sec)') plt.savefig('tclab_dyn_meas1.png')
plt.show() (:sourceend:) (:divend:)
(:toggle hide gekko_labAf button show="Lab A: Python GEKKO Energy Balance":) (:div id=gekko_labAf:)
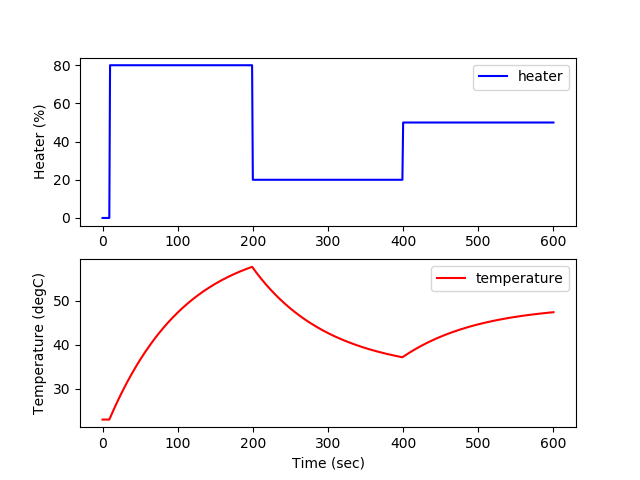
(:source lang=python:) import numpy as np import matplotlib.pyplot as plt from gekko import GEKKO
- initialize GEKKO model
m = GEKKO()
- model discretized time
n = 60*10+1 # Number of second time points (10min) m.time = np.linspace(0,n-1,n) # Time vector
- Parameters
Qd = np.zeros(601) Qd[10:200] = 80 Qd[200:400] = 20 Qd[400:] = 50 Q = m.Param(value=Qd) # Percent Heater (0-100%)
T0 = m.Param(value=23.0+273.15) # Initial temperature Ta = m.Param(value=23.0+273.15) # K U = m.Param(value=10.0) # W/m^2-K mass = m.Param(value=4.0/1000.0) # kg Cp = m.Param(value=0.5*1000.0) # J/kg-K A = m.Param(value=12.0/100.0**2) # Area in m^2 alpha = m.Param(value=0.01) # W / % heater eps = m.Param(value=0.9) # Emissivity sigma = m.Const(5.67e-8) # Stefan-Boltzman
T = m.Var(value=T0) #Temperature state as GEKKO variable
m.Equation(T.dt() == (1.0/(mass*Cp))*(U*A*(Ta-T) + eps * sigma * A * (Ta**4 - T**4) + alpha*Q))
- simulation mode
m.options.IMODE = 4
- simulation model
m.solve()
- plot results
plt.figure(1) plt.subplot(2,1,1) plt.plot(m.time,Q.value,'b-',label='heater') plt.ylabel('Heater (%)') plt.legend(loc='best') plt.subplot(2,1,2) plt.plot(m.time,np.array(T.value)-273.15,'r-',label='temperature') plt.ylabel('Temperature (degC)') plt.legend(loc='best') plt.xlabel('Time (sec)') plt.savefig('tclab_eb_pred.png') plt.show() (:sourceend:) (:divend:)
(:toggle hide gekko_labAe button show="Lab A: Python GEKKO Neural Network":) (:div id=gekko_labAe:)
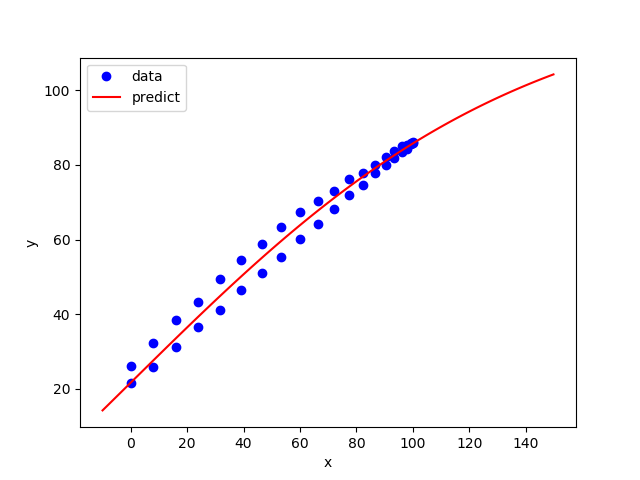
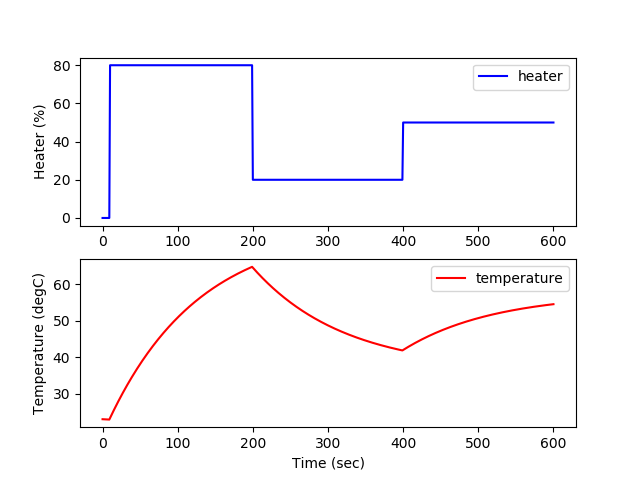
(:source lang=python:) import numpy as np import pandas as pd import matplotlib.pyplot as plt from gekko import GEKKO import time
- -------------------------------------
- import or generate data
- -------------------------------------
filename = 'tclab_ss_data1.csv' try:
try:
data = pd.read_csv(filename)
except:
url = 'https://apmonitor.com/do/uploads/Main/tclab_ss_data1.txt'
data = pd.read_csv(url)
except:
# generate training data if data file not available
import tclab
# Connect to Arduino
a = tclab.TCLab()
fid = open(filename,'w')
fid.write('Heater,Temperature\n')
# test takes 2 hours = 40 pts * 3 minutes each
npts = 40
Q = np.sin(np.linspace(0,np.pi,npts))*100
for i in range(npts):
# set heater value
a.Q1(Q[i])
print('Heater 1: ' + str(Q[i]) + ' %')
# wait 3 minutes
time.sleep(3*60)
# record temperature and heater value
print('Temperature 1: ' + str(a.T1) + ' degC')
fid.write(str(Q[i])+',str(a.T1)\n')
# close file
fid.close()
# close connection to Arduino
a.close()
# read data file
data = pd.read_csv(filename)
- -------------------------------------
- scale data
- -------------------------------------
x = data['Heater'].values y = data['Temperature'].values
- minimum of x,y
x_min = min(x) y_min = min(y)
- range of x,y
x_range = max(x)-min(x) y_range = max(y)-min(y)
- scaled data
xs = (x - x_min)/x_range ys = (y - y_min)/y_range
- -------------------------------------
- build neural network
- -------------------------------------
nin = 1 # inputs n1 = 1 # hidden layer 1 (linear) n2 = 1 # hidden layer 2 (nonlinear) n3 = 1 # hidden layer 3 (linear) nout = 1 # outputs
- Initialize gekko models
train = GEKKO() test = GEKKO() dyn = GEKKO() model = [train,test,dyn]
for m in model:
# input(s)
m.inpt = m.Param()
# layer 1
m.w1 = m.Array(m.FV, (nin,n1))
m.l1 = [m.Intermediate(m.w1[0,i]*m.inpt) for i in range(n1)]
# layer 2
m.w2 = m.Array(m.FV, (n1,n2))
m.l2 = [m.Intermediate(sum([m.tanh(m.w2[j,i]*m.l1[j]) for j in range(n1)])) for i in range(n2)]
# layer 3
m.w3 = m.Array(m.FV, (n2,n3))
m.l3 = [m.Intermediate(sum([m.w3[j,i]*m.l2[j] for j in range(n2)])) for i in range(n3)]
# output(s)
m.outpt = m.CV()
m.Equation(m.outpt==sum([m.l3[i] for i in range(n3)]))
# flatten matrices
m.w1 = m.w1.flatten()
m.w2 = m.w2.flatten()
m.w3 = m.w3.flatten()
- -------------------------------------
- fit parameter weights
- -------------------------------------
m = train m.inpt.value=xs m.outpt.value=ys m.outpt.FSTATUS = 1 for i in range(len(m.w1)):
m.w1[i].FSTATUS=1
m.w1[i].STATUS=1
m.w1[i].MEAS=1.0
for i in range(len(m.w2)):
m.w2[i].STATUS=1
m.w2[i].FSTATUS=1
m.w2[i].MEAS=0.5
for i in range(len(m.w3)):
m.w3[i].FSTATUS=1
m.w3[i].STATUS=1
m.w3[i].MEAS=1.0
m.options.IMODE = 2 m.options.SOLVER = 3 m.options.EV_TYPE = 2 m.solve(disp=False)
- -------------------------------------
- test sample points
- -------------------------------------
m = test for i in range(len(m.w1)):
m.w1[i].MEAS=train.w1[i].NEWVAL
m.w1[i].FSTATUS = 1
print('w1[str(i)]: '+str(m.w1[i].MEAS))
for i in range(len(m.w2)):
m.w2[i].MEAS=train.w2[i].NEWVAL
m.w2[i].FSTATUS = 1
print('w2[str(i)]: '+str(m.w2[i].MEAS))
for i in range(len(m.w3)):
m.w3[i].MEAS=train.w3[i].NEWVAL
m.w3[i].FSTATUS = 1
print('w3[str(i)]: '+str(m.w3[i].MEAS))
m.inpt.value=np.linspace(-0.1,1.5,100) m.options.IMODE = 2 m.options.SOLVER = 3 m.solve(disp=False)
- -------------------------------------
- un-scale predictions
- -------------------------------------
xp = np.array(test.inpt.value) * x_range + x_min yp = np.array(test.outpt.value) * y_range + y_min
- -------------------------------------
- plot results
- -------------------------------------
plt.figure() plt.plot(x,y,'bo',label='data') plt.plot(xp,yp,'r-',label='predict') plt.legend(loc='best') plt.ylabel('y') plt.xlabel('x') plt.savefig('tclab_ss_data1.png')
- -------------------------------------
- generate dynamic predictions
- -------------------------------------
m = dyn m.time = np.linspace(0,600,601)
- load neural network parameters
for i in range(len(m.w1)):
m.w1[i].MEAS=train.w1[i].NEWVAL
m.w1[i].FSTATUS = 1
for i in range(len(m.w2)):
m.w2[i].MEAS=train.w2[i].NEWVAL
m.w2[i].FSTATUS = 1
for i in range(len(m.w3)):
m.w3[i].MEAS=train.w3[i].NEWVAL
m.w3[i].FSTATUS = 1
- doublet test
Qd = np.zeros(601) Qd[10:200] = 80 Qd[200:400] = 20 Qd[400:] = 50 Q = m.Param() Q.value = Qd
- scaled input
m.inpt.value = (Qd - x_min) / x_range
- define Temperature output
Q0 = 0 # initial heater T0 = 23 # initial temperature
- scaled steady state ouput
T_ss = m.Var(value=T0) m.Equation(T_ss == m.outpt*y_range + y_min)
- dynamic prediction
T = m.Var(value=T0)
- time constant
tau = m.Param(value=120) # determine in a later exercise
- additional model equation for dynamics
m.Equation(tau*T.dt()==-(T-T0)+(T_ss-T0))
- solve dynamic simulation
m.options.IMODE=4 m.solve()
plt.figure() plt.subplot(2,1,1) plt.plot(m.time,Q.value,'b-',label='heater') plt.ylabel('Heater (%)') plt.legend(loc='best') plt.subplot(2,1,2) plt.plot(m.time,T.value,'r-',label='temperature')
- plt.plot(m.time,T_ss.value,'k--',label='target temperature')
plt.ylabel('Temperature (degC)') plt.legend(loc='best') plt.xlabel('Time (sec)') plt.savefig('tclab_dyn_pred.png') plt.show() (:sourceend:) (:divend:)
Lab B
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/ZUHiQORwmxw" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> (:htmlend:)
- MIMO Energy Balance Solution with MATLAB and Python
- Steady state data, 2 heaters
- Dynamic data, 2 heaters
(:toggle hide gekko_labBd button show="Lab B: Python TCLab Generate Step Data":) (:div id=gekko_labBd:) (:source lang=python:) import numpy as np import pandas as pd import tclab import time import matplotlib.pyplot as plt
- generate step test data on Arduino
filename = 'tclab_dyn_data2.csv'
- heater steps
Q1d = np.zeros(601) Q1d[10:200] = 80 Q1d[200:280] = 20 Q1d[280:400] = 70 Q1d[400:] = 50
Q2d = np.zeros(601) Q2d[120:320] = 100 Q2d[320:520] = 10 Q2d[520:] = 80
- Connect to Arduino
a = tclab.TCLab() fid = open(filename,'w') fid.write('Time,H1,H2,T1,T2\n') fid.close()
- run step test (10 min)
for i in range(601):
# set heater values
a.Q1(Q1d[i])
a.Q2(Q2d[i])
print('Time: ' + str(i) + ' H1: ' + str(Q1d[i]) + ' H2: ' + str(Q2d[i]) + ' T1: ' + str(a.T1) + ' T2: ' + str(a.T2))
# wait 1 second
time.sleep(1)
fid = open(filename,'a')
fid.write(str(i)+',str(Q1d[i]),str(Q2d[i]),' +str(a.T1)+',str(a.T2)\n')
- close connection to Arduino
a.close()
- read data file
data = pd.read_csv(filename)
- plot measurements
plt.figure() plt.subplot(2,1,1) plt.plot(data['Time'],data['H1'],'r-',label='Heater 1') plt.plot(data['Time'],data['H2'],'b--',label='Heater 2') plt.ylabel('Heater (%)') plt.legend(loc='best') plt.subplot(2,1,2) plt.plot(data['Time'],data['T1'],'r.',label='Temperature 1') plt.plot(data['Time'],data['T2'],'b.',label='Temperature 2') plt.ylabel('Temperature (degC)') plt.legend(loc='best') plt.xlabel('Time (sec)') plt.savefig('tclab_dyn_meas2.png')
plt.show() (:sourceend:) (:divend:)
(:toggle hide gekko_labBf button show="Lab B: Python GEKKO Energy Balance":) (:div id=gekko_labBf:)
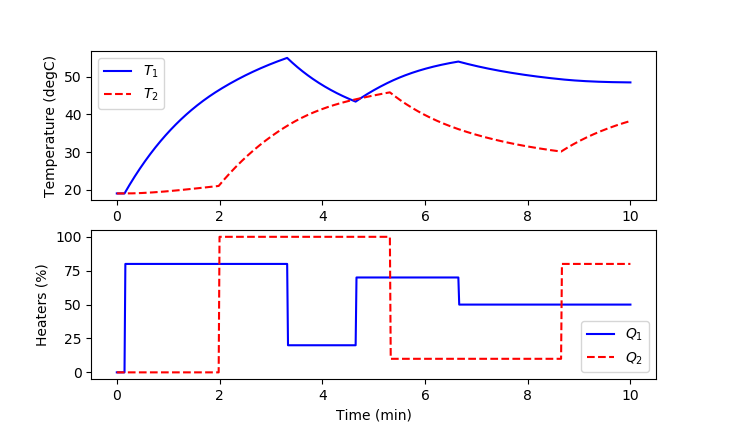
(:source lang=python:) import numpy as np import matplotlib.pyplot as plt from gekko import GEKKO
- initialize GEKKO model
m = GEKKO()
- model discretized time
n = 60*10+1 # Number of second time points (10min) m.time = np.linspace(0,n-1,n) # Time vector
- Parameters
- Percent Heater (0-100%)
Q1d = np.zeros(n) Q1d[10:200] = 80 Q1d[200:280] = 20 Q1d[280:400] = 70 Q1d[400:] = 50 Q1 = m.Param() Q1.value = Q1d
Q2d = np.zeros(n) Q2d[120:320] = 100 Q2d[320:520] = 10 Q2d[520:] = 80 Q2 = m.Param() Q2.value = Q2d# Heaters as time-varying inputs Q1 = m.Param(value=Q1d) # Percent Heater (0-100%) Q2 = m.Param(value=Q2d) # Percent Heater (0-100%)
T0 = m.Param(value=19.0+273.15) # Initial temperature Ta = m.Param(value=19.0+273.15) # K U = m.Param(value=10.0) # W/m^2-K mass = m.Param(value=4.0/1000.0) # kg Cp = m.Param(value=0.5*1000.0) # J/kg-K A = m.Param(value=10.0/100.0**2) # Area not between heaters in m^2 As = m.Param(value=2.0/100.0**2) # Area between heaters in m^2 alpha1 = m.Param(value=0.01) # W / % heater alpha2 = m.Param(value=0.005) # W / % heater eps = m.Param(value=0.9) # Emissivity sigma = m.Const(5.67e-8) # Stefan-Boltzman
- Temperature states as GEKKO variables
T1 = m.Var(value=T0) T2 = m.Var(value=T0)
- Between two heaters
Q_C12 = m.Intermediate(U*As*(T2-T1)) # Convective Q_R12 = m.Intermediate(eps*sigma*As*(T2**4-T1**4)) # Radiative
m.Equation(T1.dt() == (1.0/(mass*Cp))*(U*A*(Ta-T1) + eps * sigma * A * (Ta**4 - T1**4) + Q_C12 + Q_R12 + alpha1*Q1))
m.Equation(T2.dt() == (1.0/(mass*Cp))*(U*A*(Ta-T2) + eps * sigma * A * (Ta**4 - T2**4) - Q_C12 - Q_R12 + alpha2*Q2))
- simulation mode
m.options.IMODE = 4
- simulation model
m.solve()
- plot results
plt.figure(1) plt.subplot(2,1,1) plt.plot(m.time/60.0,np.array(T1.value)-273.15,'b-') plt.plot(m.time/60.0,np.array(T2.value)-273.15,'r--') plt.legend([r'$T_1$',r'$T_2$'],loc='best') plt.ylabel('Temperature (degC)')
plt.subplot(2,1,2) plt.plot(m.time/60.0,np.array(Q1.value),'b-') plt.plot(m.time/60.0,np.array(Q2.value),'r--') plt.legend([r'$Q_1$',r'$Q_2$'],loc='best') plt.ylabel('Heaters (%)')
plt.xlabel('Time (min)') plt.show() (:sourceend:) (:divend:)
(:toggle hide gekko_labBnn button show="Lab B: Python GEKKO Neural Network":) (:div id=gekko_labBnn:)
(:source lang=python:) import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.preprocessing import MinMaxScaler from gekko import GEKKO
import time
- -------------------------------------
- import or generate data
- -------------------------------------
filename = 'tclab_ss_data2.csv' try:
try:
data = pd.read_csv(filename)
except:
url = 'https://apmonitor.com/do/uploads/Main/tclab_ss_data2.txt'
data = pd.read_csv(url)
except:
# generate training data if data file not available
import tclab
# Connect to Arduino
a = tclab.TCLab()
fid = open(filename,'w')
fid.write('Heater 1,Heater 2,Temperature 1,Temperature 2\n')
fid.close()
# data collection takes 6 hours = 120 pts * 3 minutes each
npts = 120
for i in range(npts):
# set random heater values
Q1 = np.random.rand()*100
Q2 = np.random.rand()*100
a.Q1(Q1)
a.Q2(Q2)
print('Heater 1: ' + str(Q1) + ' %')
print('Heater 2: ' + str(Q2) + ' %')
# wait 3 minutes
time.sleep(3*60)
# record temperature and heater value
print('Temperature 1: ' + str(a.T1) + ' degC')
print('Temperature 2: ' + str(a.T2) + ' degC')
fid = open(filename,'a')
fid.write(str(Q1)+',str(Q2),str(a.T1),str(a.T2)\n')
fid.close()
# close connection to Arduino
a.close()
# read data file
data = pd.read_csv(filename)
- -------------------------------------
- scale data
- -------------------------------------
s = MinMaxScaler(feature_range=(0,1)) sc_train = s.fit_transform(data)
- partition into inputs and outputs
xs = sc_train[:,0:2] # 2 heaters ys = sc_train[:,2:4] # 2 temperatures
- -------------------------------------
- build neural network
- -------------------------------------
nin = 2 # inputs n1 = 2 # hidden layer 1 (linear) n2 = 2 # hidden layer 2 (nonlinear) n3 = 2 # hidden layer 3 (linear) nout = 2 # outputs
- Initialize gekko models
train = GEKKO() dyn = GEKKO() model = [train,dyn]
for m in model:
# use APOPT solver
m.options.SOLVER = 1
# input(s)
m.inpt = [m.Param() for i in range(nin)]
# layer 1 (linear)
m.w1 = m.Array(m.FV, (nout,nin,n1))
m.l1 = [[m.Intermediate(sum([m.w1[k,j,i]*m.inpt[j] for j in range(nin)])) for i in range(n1)] for k in range(nout)]
# layer 2 (tanh)
m.w2 = m.Array(m.FV, (nout,n1,n2))
m.l2 = [[m.Intermediate(sum([m.tanh(m.w2[k,j,i]*m.l1[k][j]) for j in range(n1)])) for i in range(n2)] for k in range(nout)]
# layer 3 (linear)
m.w3 = m.Array(m.FV, (nout,n2,n3))
m.l3 = [[m.Intermediate(sum([m.w3[k,j,i]*m.l2[k][j] for j in range(n2)])) for i in range(n3)] for k in range(nout)]
# outputs
m.outpt = [m.CV() for i in range(nout)]
m.Equations([m.outpt[k]==sum([m.l3[k][i] for i in range(n3)]) for k in range(nout)])
# flatten matrices
m.w1 = m.w1.flatten()
m.w2 = m.w2.flatten()
m.w3 = m.w3.flatten()
- -------------------------------------
- fit parameter weights
- -------------------------------------
m = train for i in range(nin):
m.inpt[i].value=xs[:,i]
for i in range(nout):
m.outpt[i].value = ys[:,i]
m.outpt[i].FSTATUS = 1
for i in range(len(m.w1)):
m.w1[i].FSTATUS=1
m.w1[i].STATUS=1
m.w1[i].MEAS=1.0
for i in range(len(m.w2)):
m.w2[i].STATUS=1
m.w2[i].FSTATUS=1
m.w2[i].MEAS=0.5
for i in range(len(m.w3)):
m.w3[i].FSTATUS=1
m.w3[i].STATUS=1
m.w3[i].MEAS=1.0
m.options.IMODE = 2 m.options.EV_TYPE = 2
- solve for weights to minimize loss (objective)
m.solve(disp=True)
- -------------------------------------
- generate dynamic predictions
- -------------------------------------
m = dyn tf = 600 m.time = np.linspace(0,tf,tf+1)
- load neural network parameters
for i in range(len(m.w1)):
m.w1[i].MEAS=train.w1[i].NEWVAL
m.w1[i].FSTATUS = 1
for i in range(len(m.w2)):
m.w2[i].MEAS=train.w2[i].NEWVAL
m.w2[i].FSTATUS = 1
for i in range(len(m.w3)):
m.w3[i].MEAS=train.w3[i].NEWVAL
m.w3[i].FSTATUS = 1
- step tests
Q1d = np.zeros(tf+1) Q1d[10:200] = 80 Q1d[200:280] = 20 Q1d[280:400] = 70 Q1d[400:] = 50 Q1 = m.Param() Q1.value = Q1d
Q2d = np.zeros(tf+1) Q2d[120:320] = 100 Q2d[320:520] = 10 Q2d[520:] = 80 Q2 = m.Param() Q2.value = Q2d
- scaled inputs
m.inpt[0].value = Q1d * s.scale_[0] + s.min_[0] m.inpt[1].value = Q2d * s.scale_[1] + s.min_[1]
- define Temperature output
Q0 = 0 # initial heater T0 = 19 # ambient temperature
- scaled steady state ouput
T1_ss = m.Var(value=T0) T2_ss = m.Var(value=T0) m.Equation(T1_ss == (m.outpt[0]-s.min_[2])/s.scale_[2]) m.Equation(T2_ss == (m.outpt[1]-s.min_[3])/s.scale_[3])
- dynamic prediction
T1 = m.Var(value=T0) T2 = m.Var(value=T0)
- time constant
tau = m.Param(value=120) # determine in a later exercise
- additional model equation for dynamics
m.Equation(tau*T1.dt()==-(T1-T0)+(T1_ss-T0)) m.Equation(tau*T2.dt()==-(T2-T0)+(T2_ss-T0))
- solve dynamic simulation
m.options.IMODE=4 m.solve()
- generate step test data on Arduino
- -------------------------------------
- import or generate data
- -------------------------------------
filename = 'tclab_dyn_data2.csv' try:
try:
data = pd.read_csv(filename)
except:
url = 'https://apmonitor.com/do/uploads/Main/tclab_dyn_data2.txt'
data = pd.read_csv(url)
except:
# generate training data if data file not available
import tclab
# Connect to Arduino
a = tclab.TCLab()
fid = open(filename,'w')
fid.write('Time,H1,H2,T1,T2\n')
fid.close()
# check for cool down
i = 0
while i<=10:
i += 1 # upper limit on wait time
T1m = a.T1
T2m = a.T2
print('T1: ' + str(a.T1) + ' T2: ' + str(a.T2))
print('Sleep 30 sec')
time.sleep(30)
if (a.T1<30 and a.T2<30 and a.T1>=T1m-0.2 and a.T2>=T2m-0.2):
break # continue when conditions met
else:
print('Not at ambient temperature')
# run step test (10 min)
for i in range(tf+1):
# set heater values
a.Q1(Q1d[i])
a.Q2(Q2d[i])
print('Time: ' + str(i) + ' H1: ' + str(Q1d[i]) + ' H2: ' + str(Q2d[i]) + ' T1: ' + str(a.T1) + ' T2: ' + str(a.T2))
# wait 1 second
time.sleep(1)
fid = open(filename,'a')
fid.write(str(i)+',str(Q1d[i]),str(Q2d[i]),' +str(a.T1)+',str(a.T2)\n')
fid.close()
# close connection to Arduino
a.close()
# read data file
data = pd.read_csv(filename)
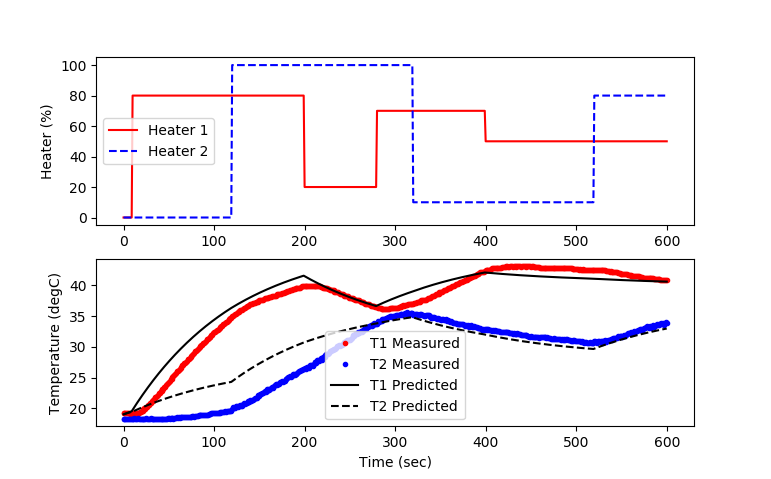
- plot prediction and measurement
plt.figure() plt.subplot(2,1,1) plt.plot(m.time,Q1.value,'r-',label='Heater 1') plt.plot(m.time,Q2.value,'b--',label='Heater 2') plt.ylabel('Heater (%)') plt.legend(loc='best') plt.subplot(2,1,2) plt.plot(data['Time'],data['T1'],'r.',label='T1 Measured') plt.plot(data['Time'],data['T2'],'b.',label='T2 Measured') plt.plot(m.time,T1.value,'k-',label='T1 Predicted') plt.plot(m.time,T2.value,'k--',label='T2 Predicted') plt.ylabel('Temperature (degC)') plt.legend(loc='best') plt.xlabel('Time (sec)') plt.savefig('tclab_dyn_pred.png')
plt.show() (:sourceend:) (:divend:)
Lab C
- Parameter Estimation with MATLAB (fmincon), Python (Scipy or GEKKO)
Lab D
- Solution
Lab E
- Solution
Lab F
- Solution with Python
- Solution with MATLAB
Lab G
- Solution with MATLAB and Python
Lab H
- Solution
- Parameter Estimation with MATLAB (fmincon), Python (Scipy or GEKKO)
<iframe width="560" height="315" src="https://www.youtube.com/embed/g1w5vvpj-a0" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe>
<iframe width="560" height="315" src="https://www.youtube.com/embed/ZUHiQORwmxw" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe>
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/g1w5vvpj-a0" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> (:htmlend:)
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/SomZYxmIDE8" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> (:htmlend:)
This Arduino lab is a hands-on applications of advanced temperature control with two heaters and two temperature sensors. The labs reinforce principles of model development, estimation, and advanced control methods.
This Arduino lab is a hands-on application of machine learning and advanced temperature control with two heaters and two temperature sensors. The labs reinforce principles of model development, estimation, and advanced control methods.
(:toggle hide gekko_labAd button show="Lab A: Python TCLab Step Data":)
(:toggle hide gekko_labAd button show="Lab A: Python TCLab Generate Step Data":)
(:toggle hide gekko_labBd button show="Lab B: Python TCLab Step Data":)
(:toggle hide gekko_labBd button show="Lab B: Python TCLab Generate Step Data":)
(:toggle hide gekko_labBd button show="Lab A: Python TCLab Step Data":)
(:toggle hide gekko_labBd button show="Lab B: Python TCLab Step Data":)
(:toggle hide gekko_labAf button show="Lab A: Python GEKKO Energy Balance":) (:div id=gekko_labAf:)

(:toggle hide gekko_labAd button show="Lab A: Python TCLab Step Data":) (:div id=gekko_labAd:)
import pandas as pd import tclab import time
from gekko import GEKKO
- initialize GEKKO model
m = GEKKO()
- model discretized time
n = 60*10+1 # Number of second time points (10min) m.time = np.linspace(0,n-1,n) # Time vector
- Parameters
- generate step test data on Arduino
filename = 'tclab_dyn_data1.csv'
- heater steps
Q = m.Param(value=Qd) # Percent Heater (0-100%)
T0 = m.Param(value=23.0+273.15) # Initial temperature Ta = m.Param(value=23.0+273.15) # K U = m.Param(value=10.0) # W/m^2-K mass = m.Param(value=4.0/1000.0) # kg Cp = m.Param(value=0.5*1000.0) # J/kg-K A = m.Param(value=12.0/100.0**2) # Area in m^2 alpha = m.Param(value=0.01) # W / % heater eps = m.Param(value=0.9) # Emissivity sigma = m.Const(5.67e-8) # Stefan-Boltzman
T = m.Var(value=T0) #Temperature state as GEKKO variable
m.Equation(T.dt() == (1.0/(mass*Cp))*(U*A*(Ta-T) + eps * sigma * A * (Ta**4 - T**4) + alpha*Q))
- simulation mode
m.options.IMODE = 4
- simulation model
m.solve()
- plot results
plt.figure(1)
- Connect to Arduino
a = tclab.TCLab() fid = open(filename,'w') fid.write('Time,H1,T1\n') fid.close()
- run step test (10 min)
for i in range(601):
# set heater value
a.Q1(Qd[i])
print('Time: ' + str(i) + ' H1: ' + str(Qd[i]) + ' T1: ' + str(a.T1))
# wait 1 second
time.sleep(1)
# write results to file
fid = open(filename,'a')
fid.write(str(i)+',str(Qd[i]),str(a.T1)\n')
fid.close()
- close connection to Arduino
a.close()
- read data file
data = pd.read_csv(filename)
- plot measurements
plt.figure()
plt.plot(m.time,Q.value,'b-',label='heater')
plt.plot(data['Time'],data['H1'],'b-',label='Heater 1')
plt.plot(m.time,np.array(T.value)-273.15,'r-',label='temperature')
plt.plot(data['Time'],data['T1'],'r.',label='Temperature 1')
plt.savefig('tclab_eb_pred.png')
plt.savefig('tclab_dyn_meas1.png')
(:toggle hide gekko_labAe button show="Lab A: Python GEKKO Neural Network":) (:div id=gekko_labAe:)


(:toggle hide gekko_labAf button show="Lab A: Python GEKKO Energy Balance":) (:div id=gekko_labAf:)

import pandas as pd import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
- initialize GEKKO model
m = GEKKO()
- model discretized time
n = 60*10+1 # Number of second time points (10min) m.time = np.linspace(0,n-1,n) # Time vector
- Parameters
Qd = np.zeros(601) Qd[10:200] = 80 Qd[200:400] = 20 Qd[400:] = 50 Q = m.Param(value=Qd) # Percent Heater (0-100%)
T0 = m.Param(value=23.0+273.15) # Initial temperature Ta = m.Param(value=23.0+273.15) # K U = m.Param(value=10.0) # W/m^2-K mass = m.Param(value=4.0/1000.0) # kg Cp = m.Param(value=0.5*1000.0) # J/kg-K A = m.Param(value=12.0/100.0**2) # Area in m^2 alpha = m.Param(value=0.01) # W / % heater eps = m.Param(value=0.9) # Emissivity sigma = m.Const(5.67e-8) # Stefan-Boltzman
T = m.Var(value=T0) #Temperature state as GEKKO variable
m.Equation(T.dt() == (1.0/(mass*Cp))*(U*A*(Ta-T) + eps * sigma * A * (Ta**4 - T**4) + alpha*Q))
- simulation mode
m.options.IMODE = 4
- simulation model
m.solve()
- plot results
plt.figure(1) plt.subplot(2,1,1) plt.plot(m.time,Q.value,'b-',label='heater') plt.ylabel('Heater (%)') plt.legend(loc='best') plt.subplot(2,1,2) plt.plot(m.time,np.array(T.value)-273.15,'r-',label='temperature') plt.ylabel('Temperature (degC)') plt.legend(loc='best') plt.xlabel('Time (sec)') plt.savefig('tclab_eb_pred.png') plt.show() (:sourceend:) (:divend:)
(:toggle hide gekko_labAe button show="Lab A: Python GEKKO Neural Network":) (:div id=gekko_labAe:)


(:source lang=python:) import numpy as np import pandas as pd import matplotlib.pyplot as plt from gekko import GEKKO
(:toggle hide gekko_labBd button show="Lab A: Python TCLab Step Data":) (:div id=gekko_labBd:) (:source lang=python:) import numpy as np import pandas as pd import tclab import time import matplotlib.pyplot as plt
- generate step test data on Arduino
filename = 'tclab_dyn_data2.csv'
- heater steps
Q1d = np.zeros(601) Q1d[10:200] = 80 Q1d[200:280] = 20 Q1d[280:400] = 70 Q1d[400:] = 50
Q2d = np.zeros(601) Q2d[120:320] = 100 Q2d[320:520] = 10 Q2d[520:] = 80
- Connect to Arduino
a = tclab.TCLab() fid = open(filename,'w') fid.write('Time,H1,H2,T1,T2\n') fid.close()
- run step test (10 min)
for i in range(601):
# set heater values
a.Q1(Q1d[i])
a.Q2(Q2d[i])
print('Time: ' + str(i) + ' H1: ' + str(Q1d[i]) + ' H2: ' + str(Q2d[i]) + ' T1: ' + str(a.T1) + ' T2: ' + str(a.T2))
# wait 1 second
time.sleep(1)
fid = open(filename,'a')
fid.write(str(i)+',str(Q1d[i]),str(Q2d[i]),' +str(a.T1)+',str(a.T2)\n')
- close connection to Arduino
a.close()
- read data file
data = pd.read_csv(filename)
- plot measurements
plt.figure() plt.subplot(2,1,1) plt.plot(data['Time'],data['H1'],'r-',label='Heater 1') plt.plot(data['Time'],data['H2'],'b--',label='Heater 2') plt.ylabel('Heater (%)') plt.legend(loc='best') plt.subplot(2,1,2) plt.plot(data['Time'],data['T1'],'r.',label='Temperature 1') plt.plot(data['Time'],data['T2'],'b.',label='Temperature 2') plt.ylabel('Temperature (degC)') plt.legend(loc='best') plt.xlabel('Time (sec)') plt.savefig('tclab_dyn_meas2.png')
plt.show() (:sourceend:) (:divend:)
- Solution with MATLAB and Python
- SISO Energy Balance Solution with MATLAB and Python
- Solution
- MIMO Energy Balance Solution with MATLAB and Python
(:toggle hide gekko_labBf button show="Lab A: Python GEKKO Energy Balance":)
(:toggle hide gekko_labBf button show="Lab B: Python GEKKO Energy Balance":)
(:toggle hide gekko_labBf button show="Lab A: Python GEKKO Neural Network":) (:div id=gekko_labBf:)
(:toggle hide gekko_labBnn button show="Lab B: Python GEKKO Neural Network":) (:div id=gekko_labBnn:)
(:toggle hide gekko_labBf button show="Lab A: Python GEKKO Energy Balance":) (:div id=gekko_labBf:)

(:source lang=python:) import numpy as np import matplotlib.pyplot as plt from gekko import GEKKO
- initialize GEKKO model
m = GEKKO()
- model discretized time
n = 60*10+1 # Number of second time points (10min) m.time = np.linspace(0,n-1,n) # Time vector
- Parameters
- Percent Heater (0-100%)
Q1d = np.zeros(n) Q1d[10:200] = 80 Q1d[200:280] = 20 Q1d[280:400] = 70 Q1d[400:] = 50 Q1 = m.Param() Q1.value = Q1d
Q2d = np.zeros(n) Q2d[120:320] = 100 Q2d[320:520] = 10 Q2d[520:] = 80 Q2 = m.Param() Q2.value = Q2d# Heaters as time-varying inputs Q1 = m.Param(value=Q1d) # Percent Heater (0-100%) Q2 = m.Param(value=Q2d) # Percent Heater (0-100%)
T0 = m.Param(value=19.0+273.15) # Initial temperature Ta = m.Param(value=19.0+273.15) # K U = m.Param(value=10.0) # W/m^2-K mass = m.Param(value=4.0/1000.0) # kg Cp = m.Param(value=0.5*1000.0) # J/kg-K A = m.Param(value=10.0/100.0**2) # Area not between heaters in m^2 As = m.Param(value=2.0/100.0**2) # Area between heaters in m^2 alpha1 = m.Param(value=0.01) # W / % heater alpha2 = m.Param(value=0.005) # W / % heater eps = m.Param(value=0.9) # Emissivity sigma = m.Const(5.67e-8) # Stefan-Boltzman
- Temperature states as GEKKO variables
T1 = m.Var(value=T0) T2 = m.Var(value=T0)
- Between two heaters
Q_C12 = m.Intermediate(U*As*(T2-T1)) # Convective Q_R12 = m.Intermediate(eps*sigma*As*(T2**4-T1**4)) # Radiative
m.Equation(T1.dt() == (1.0/(mass*Cp))*(U*A*(Ta-T1) + eps * sigma * A * (Ta**4 - T1**4) + Q_C12 + Q_R12 + alpha1*Q1))
m.Equation(T2.dt() == (1.0/(mass*Cp))*(U*A*(Ta-T2) + eps * sigma * A * (Ta**4 - T2**4) - Q_C12 - Q_R12 + alpha2*Q2))
- simulation mode
m.options.IMODE = 4
- simulation model
m.solve()
- plot results
plt.figure(1) plt.subplot(2,1,1) plt.plot(m.time/60.0,np.array(T1.value)-273.15,'b-') plt.plot(m.time/60.0,np.array(T2.value)-273.15,'r--') plt.legend([r'$T_1$',r'$T_2$'],loc='best') plt.ylabel('Temperature (degC)')
plt.subplot(2,1,2) plt.plot(m.time/60.0,np.array(Q1.value),'b-') plt.plot(m.time/60.0,np.array(Q2.value),'r--') plt.legend([r'$Q_1$',r'$Q_2$'],loc='best') plt.ylabel('Heaters (%)')
plt.xlabel('Time (min)') plt.show() (:sourceend:) (:divend:)
(:toggle hide gekko_labBf button show="Lab A: Python GEKKO Neural Network":) (:div id=gekko_labBf:)

(:source lang=python:) import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.preprocessing import MinMaxScaler from gekko import GEKKO
import time
- -------------------------------------
- import or generate data
- -------------------------------------
filename = 'tclab_ss_data2.csv' try:
try:
data = pd.read_csv(filename)
except:
url = 'https://apmonitor.com/do/uploads/Main/tclab_ss_data2.txt'
data = pd.read_csv(url)
except:
# generate training data if data file not available
import tclab
# Connect to Arduino
a = tclab.TCLab()
fid = open(filename,'w')
fid.write('Heater 1,Heater 2,Temperature 1,Temperature 2\n')
fid.close()
# data collection takes 6 hours = 120 pts * 3 minutes each
npts = 120
for i in range(npts):
# set random heater values
Q1 = np.random.rand()*100
Q2 = np.random.rand()*100
a.Q1(Q1)
a.Q2(Q2)
print('Heater 1: ' + str(Q1) + ' %')
print('Heater 2: ' + str(Q2) + ' %')
# wait 3 minutes
time.sleep(3*60)
# record temperature and heater value
print('Temperature 1: ' + str(a.T1) + ' degC')
print('Temperature 2: ' + str(a.T2) + ' degC')
fid = open(filename,'a')
fid.write(str(Q1)+',str(Q2),str(a.T1),str(a.T2)\n')
fid.close()
# close connection to Arduino
a.close()
# read data file
data = pd.read_csv(filename)
- -------------------------------------
- scale data
- -------------------------------------
s = MinMaxScaler(feature_range=(0,1)) sc_train = s.fit_transform(data)
- partition into inputs and outputs
xs = sc_train[:,0:2] # 2 heaters ys = sc_train[:,2:4] # 2 temperatures
- -------------------------------------
- build neural network
- -------------------------------------
nin = 2 # inputs n1 = 2 # hidden layer 1 (linear) n2 = 2 # hidden layer 2 (nonlinear) n3 = 2 # hidden layer 3 (linear) nout = 2 # outputs
- Initialize gekko models
train = GEKKO() dyn = GEKKO() model = [train,dyn]
for m in model:
# use APOPT solver
m.options.SOLVER = 1
# input(s)
m.inpt = [m.Param() for i in range(nin)]
# layer 1 (linear)
m.w1 = m.Array(m.FV, (nout,nin,n1))
m.l1 = [[m.Intermediate(sum([m.w1[k,j,i]*m.inpt[j] for j in range(nin)])) for i in range(n1)] for k in range(nout)]
# layer 2 (tanh)
m.w2 = m.Array(m.FV, (nout,n1,n2))
m.l2 = [[m.Intermediate(sum([m.tanh(m.w2[k,j,i]*m.l1[k][j]) for j in range(n1)])) for i in range(n2)] for k in range(nout)]
# layer 3 (linear)
m.w3 = m.Array(m.FV, (nout,n2,n3))
m.l3 = [[m.Intermediate(sum([m.w3[k,j,i]*m.l2[k][j] for j in range(n2)])) for i in range(n3)] for k in range(nout)]
# outputs
m.outpt = [m.CV() for i in range(nout)]
m.Equations([m.outpt[k]==sum([m.l3[k][i] for i in range(n3)]) for k in range(nout)])
# flatten matrices
m.w1 = m.w1.flatten()
m.w2 = m.w2.flatten()
m.w3 = m.w3.flatten()
- -------------------------------------
- fit parameter weights
- -------------------------------------
m = train for i in range(nin):
m.inpt[i].value=xs[:,i]
for i in range(nout):
m.outpt[i].value = ys[:,i]
m.outpt[i].FSTATUS = 1
for i in range(len(m.w1)):
m.w1[i].FSTATUS=1
m.w1[i].STATUS=1
m.w1[i].MEAS=1.0
for i in range(len(m.w2)):
m.w2[i].STATUS=1
m.w2[i].FSTATUS=1
m.w2[i].MEAS=0.5
for i in range(len(m.w3)):
m.w3[i].FSTATUS=1
m.w3[i].STATUS=1
m.w3[i].MEAS=1.0
m.options.IMODE = 2 m.options.EV_TYPE = 2
- solve for weights to minimize loss (objective)
m.solve(disp=True)
- -------------------------------------
- generate dynamic predictions
- -------------------------------------
m = dyn tf = 600 m.time = np.linspace(0,tf,tf+1)
- load neural network parameters
for i in range(len(m.w1)):
m.w1[i].MEAS=train.w1[i].NEWVAL
m.w1[i].FSTATUS = 1
for i in range(len(m.w2)):
m.w2[i].MEAS=train.w2[i].NEWVAL
m.w2[i].FSTATUS = 1
for i in range(len(m.w3)):
m.w3[i].MEAS=train.w3[i].NEWVAL
m.w3[i].FSTATUS = 1
- step tests
Q1d = np.zeros(tf+1) Q1d[10:200] = 80 Q1d[200:280] = 20 Q1d[280:400] = 70 Q1d[400:] = 50 Q1 = m.Param() Q1.value = Q1d
Q2d = np.zeros(tf+1) Q2d[120:320] = 100 Q2d[320:520] = 10 Q2d[520:] = 80 Q2 = m.Param() Q2.value = Q2d
- scaled inputs
m.inpt[0].value = Q1d * s.scale_[0] + s.min_[0] m.inpt[1].value = Q2d * s.scale_[1] + s.min_[1]
- define Temperature output
Q0 = 0 # initial heater T0 = 19 # ambient temperature
- scaled steady state ouput
T1_ss = m.Var(value=T0) T2_ss = m.Var(value=T0) m.Equation(T1_ss == (m.outpt[0]-s.min_[2])/s.scale_[2]) m.Equation(T2_ss == (m.outpt[1]-s.min_[3])/s.scale_[3])
- dynamic prediction
T1 = m.Var(value=T0) T2 = m.Var(value=T0)
- time constant
tau = m.Param(value=120) # determine in a later exercise
- additional model equation for dynamics
m.Equation(tau*T1.dt()==-(T1-T0)+(T1_ss-T0)) m.Equation(tau*T2.dt()==-(T2-T0)+(T2_ss-T0))
- solve dynamic simulation
m.options.IMODE=4 m.solve()
- generate step test data on Arduino
- -------------------------------------
- import or generate data
- -------------------------------------
filename = 'tclab_dyn_data2.csv' try:
try:
data = pd.read_csv(filename)
except:
url = 'https://apmonitor.com/do/uploads/Main/tclab_dyn_data2.txt'
data = pd.read_csv(url)
except:
# generate training data if data file not available
import tclab
# Connect to Arduino
a = tclab.TCLab()
fid = open(filename,'w')
fid.write('Time,H1,H2,T1,T2\n')
fid.close()
# check for cool down
i = 0
while i<=10:
i += 1 # upper limit on wait time
T1m = a.T1
T2m = a.T2
print('T1: ' + str(a.T1) + ' T2: ' + str(a.T2))
print('Sleep 30 sec')
time.sleep(30)
if (a.T1<30 and a.T2<30 and a.T1>=T1m-0.2 and a.T2>=T2m-0.2):
break # continue when conditions met
else:
print('Not at ambient temperature')
# run step test (10 min)
for i in range(tf+1):
# set heater values
a.Q1(Q1d[i])
a.Q2(Q2d[i])
print('Time: ' + str(i) + ' H1: ' + str(Q1d[i]) + ' H2: ' + str(Q2d[i]) + ' T1: ' + str(a.T1) + ' T2: ' + str(a.T2))
# wait 1 second
time.sleep(1)
fid = open(filename,'a')
fid.write(str(i)+',str(Q1d[i]),str(Q2d[i]),' +str(a.T1)+',str(a.T2)\n')
fid.close()
# close connection to Arduino
a.close()
# read data file
data = pd.read_csv(filename)
- plot prediction and measurement
plt.figure() plt.subplot(2,1,1) plt.plot(m.time,Q1.value,'r-',label='Heater 1') plt.plot(m.time,Q2.value,'b--',label='Heater 2') plt.ylabel('Heater (%)') plt.legend(loc='best') plt.subplot(2,1,2) plt.plot(data['Time'],data['T1'],'r.',label='T1 Measured') plt.plot(data['Time'],data['T2'],'b.',label='T2 Measured') plt.plot(m.time,T1.value,'k-',label='T1 Predicted') plt.plot(m.time,T2.value,'k--',label='T2 Predicted') plt.ylabel('Temperature (degC)') plt.legend(loc='best') plt.xlabel('Time (sec)') plt.savefig('tclab_dyn_pred.png')
plt.show() (:sourceend:) (:divend:)
Q = m.Param(value=100.0) # Percent Heater (0-100%)
Qd = np.zeros(601) Qd[10:200] = 80 Qd[200:400] = 20 Qd[400:] = 50 Q = m.Param(value=Qd) # Percent Heater (0-100%)
plt.plot(m.time/60.0,np.array(T.value)-273.15,'b-')
plt.subplot(2,1,1) plt.plot(m.time,Q.value,'b-',label='heater') plt.ylabel('Heater (%)') plt.legend(loc='best') plt.subplot(2,1,2) plt.plot(m.time,np.array(T.value)-273.15,'r-',label='temperature')
plt.xlabel('Time (min)') plt.legend(['Step Test (0-100% heater)'])
plt.legend(loc='best') plt.xlabel('Time (sec)') plt.savefig('tclab_eb_pred.png')
- Solution
- Solution with MATLAB and Python
(:toggle hide gekko_labA button show="Lab A: Python GEKKO Neural Network":) (:div id=gekko_labA:)
(:toggle hide gekko_labAf button show="Lab A: Python GEKKO Energy Balance":) (:div id=gekko_labAf:)

(:source lang=python:) import numpy as np import matplotlib.pyplot as plt from gekko import GEKKO
- initialize GEKKO model
m = GEKKO()
- model discretized time
n = 60*10+1 # Number of second time points (10min) m.time = np.linspace(0,n-1,n) # Time vector
- Parameters
Q = m.Param(value=100.0) # Percent Heater (0-100%)
T0 = m.Param(value=23.0+273.15) # Initial temperature Ta = m.Param(value=23.0+273.15) # K U = m.Param(value=10.0) # W/m^2-K mass = m.Param(value=4.0/1000.0) # kg Cp = m.Param(value=0.5*1000.0) # J/kg-K A = m.Param(value=12.0/100.0**2) # Area in m^2 alpha = m.Param(value=0.01) # W / % heater eps = m.Param(value=0.9) # Emissivity sigma = m.Const(5.67e-8) # Stefan-Boltzman
T = m.Var(value=T0) #Temperature state as GEKKO variable
m.Equation(T.dt() == (1.0/(mass*Cp))*(U*A*(Ta-T) + eps * sigma * A * (Ta**4 - T**4) + alpha*Q))
- simulation mode
m.options.IMODE = 4
- simulation model
m.solve()
- plot results
plt.figure(1) plt.plot(m.time/60.0,np.array(T.value)-273.15,'b-') plt.ylabel('Temperature (degC)') plt.xlabel('Time (min)') plt.legend(['Step Test (0-100% heater)']) plt.show() (:sourceend:) (:divend:)
(:toggle hide gekko_labAe button show="Lab A: Python GEKKO Neural Network":) (:div id=gekko_labAe:)
- Lab B - Dual Heater Modeling and Solution
- Lab C - Parameter Estimation and Solution
- Lab D - Empirical Model Estimation and Solution
- Lab E - Hybrid Model Estimation and Solution
- Lab F - Linear Model Predictive Control with Python and MATLAB
- Lab G - Nonlinear Model Predictive Control with MATLAB and Python
Lab Problem Statements
- Lab A - Single Heater Modeling and Solution
Additional Data and Solutions
Lab B
- Solution
Lab C
- Solution
Lab D
- Solution
Lab E
- Solution
Lab F
- Solution with Python
- Solution with MATLAB
Lab G
- Solution with MATLAB and Python
Lab H
url = 'https://apmonitor.com/do/uploads/Main/tclab_ss_data1.csv'
url = 'https://apmonitor.com/do/uploads/Main/tclab_ss_data1.txt'
Machine Learning Data and Solutions
Additional Data and Solutions
(:toggle hide gekko_labA button show="Lab A: Python GEKKO Neural Network":) (:div id=gekko_labA:)


(:source lang=python:) import numpy as np import pandas as pd import matplotlib.pyplot as plt from gekko import GEKKO import time
- -------------------------------------
- import or generate data
- -------------------------------------
filename = 'tclab_ss_data1.csv' try:
try:
data = pd.read_csv(filename)
except:
url = 'https://apmonitor.com/do/uploads/Main/tclab_ss_data1.csv'
data = pd.read_csv(url)
except:
# generate training data if data file not available
import tclab
# Connect to Arduino
a = tclab.TCLab()
fid = open(filename,'w')
fid.write('Heater,Temperature\n')
# test takes 2 hours = 40 pts * 3 minutes each
npts = 40
Q = np.sin(np.linspace(0,np.pi,npts))*100
for i in range(npts):
# set heater value
a.Q1(Q[i])
print('Heater 1: ' + str(Q[i]) + ' %')
# wait 3 minutes
time.sleep(3*60)
# record temperature and heater value
print('Temperature 1: ' + str(a.T1) + ' degC')
fid.write(str(Q[i])+',str(a.T1)\n')
# close file
fid.close()
# close connection to Arduino
a.close()
# read data file
data = pd.read_csv(filename)
- -------------------------------------
- scale data
- -------------------------------------
x = data['Heater'].values y = data['Temperature'].values
- minimum of x,y
x_min = min(x) y_min = min(y)
- range of x,y
x_range = max(x)-min(x) y_range = max(y)-min(y)
- scaled data
xs = (x - x_min)/x_range ys = (y - y_min)/y_range
- -------------------------------------
- build neural network
- -------------------------------------
nin = 1 # inputs n1 = 1 # hidden layer 1 (linear) n2 = 1 # hidden layer 2 (nonlinear) n3 = 1 # hidden layer 3 (linear) nout = 1 # outputs
- Initialize gekko models
train = GEKKO() test = GEKKO() dyn = GEKKO() model = [train,test,dyn]
for m in model:
# input(s)
m.inpt = m.Param()
# layer 1
m.w1 = m.Array(m.FV, (nin,n1))
m.l1 = [m.Intermediate(m.w1[0,i]*m.inpt) for i in range(n1)]
# layer 2
m.w2 = m.Array(m.FV, (n1,n2))
m.l2 = [m.Intermediate(sum([m.tanh(m.w2[j,i]*m.l1[j]) for j in range(n1)])) for i in range(n2)]
# layer 3
m.w3 = m.Array(m.FV, (n2,n3))
m.l3 = [m.Intermediate(sum([m.w3[j,i]*m.l2[j] for j in range(n2)])) for i in range(n3)]
# output(s)
m.outpt = m.CV()
m.Equation(m.outpt==sum([m.l3[i] for i in range(n3)]))
# flatten matrices
m.w1 = m.w1.flatten()
m.w2 = m.w2.flatten()
m.w3 = m.w3.flatten()
- -------------------------------------
- fit parameter weights
- -------------------------------------
m = train m.inpt.value=xs m.outpt.value=ys m.outpt.FSTATUS = 1 for i in range(len(m.w1)):
m.w1[i].FSTATUS=1
m.w1[i].STATUS=1
m.w1[i].MEAS=1.0
for i in range(len(m.w2)):
m.w2[i].STATUS=1
m.w2[i].FSTATUS=1
m.w2[i].MEAS=0.5
for i in range(len(m.w3)):
m.w3[i].FSTATUS=1
m.w3[i].STATUS=1
m.w3[i].MEAS=1.0
m.options.IMODE = 2 m.options.SOLVER = 3 m.options.EV_TYPE = 2 m.solve(disp=False)
- -------------------------------------
- test sample points
- -------------------------------------
m = test for i in range(len(m.w1)):
m.w1[i].MEAS=train.w1[i].NEWVAL
m.w1[i].FSTATUS = 1
print('w1[str(i)]: '+str(m.w1[i].MEAS))
for i in range(len(m.w2)):
m.w2[i].MEAS=train.w2[i].NEWVAL
m.w2[i].FSTATUS = 1
print('w2[str(i)]: '+str(m.w2[i].MEAS))
for i in range(len(m.w3)):
m.w3[i].MEAS=train.w3[i].NEWVAL
m.w3[i].FSTATUS = 1
print('w3[str(i)]: '+str(m.w3[i].MEAS))
m.inpt.value=np.linspace(-0.1,1.5,100) m.options.IMODE = 2 m.options.SOLVER = 3 m.solve(disp=False)
- -------------------------------------
- un-scale predictions
- -------------------------------------
xp = np.array(test.inpt.value) * x_range + x_min yp = np.array(test.outpt.value) * y_range + y_min
- -------------------------------------
- plot results
- -------------------------------------
plt.figure() plt.plot(x,y,'bo',label='data') plt.plot(xp,yp,'r-',label='predict') plt.legend(loc='best') plt.ylabel('y') plt.xlabel('x') plt.savefig('tclab_ss_data1.png')
- -------------------------------------
- generate dynamic predictions
- -------------------------------------
m = dyn m.time = np.linspace(0,600,601)
- load neural network parameters
for i in range(len(m.w1)):
m.w1[i].MEAS=train.w1[i].NEWVAL
m.w1[i].FSTATUS = 1
for i in range(len(m.w2)):
m.w2[i].MEAS=train.w2[i].NEWVAL
m.w2[i].FSTATUS = 1
for i in range(len(m.w3)):
m.w3[i].MEAS=train.w3[i].NEWVAL
m.w3[i].FSTATUS = 1
- doublet test
Qd = np.zeros(601) Qd[10:200] = 80 Qd[200:400] = 20 Qd[400:] = 50 Q = m.Param() Q.value = Qd
- scaled input
m.inpt.value = (Qd - x_min) / x_range
- define Temperature output
Q0 = 0 # initial heater T0 = 23 # initial temperature
- scaled steady state ouput
T_ss = m.Var(value=T0) m.Equation(T_ss == m.outpt*y_range + y_min)
- dynamic prediction
T = m.Var(value=T0)
- time constant
tau = m.Param(value=120) # determine in a later exercise
- additional model equation for dynamics
m.Equation(tau*T.dt()==-(T-T0)+(T_ss-T0))
- solve dynamic simulation
m.options.IMODE=4 m.solve()
plt.figure() plt.subplot(2,1,1) plt.plot(m.time,Q.value,'b-',label='heater') plt.ylabel('Heater (%)') plt.legend(loc='best') plt.subplot(2,1,2) plt.plot(m.time,T.value,'r-',label='temperature')
- plt.plot(m.time,T_ss.value,'k--',label='target temperature')
plt.ylabel('Temperature (degC)') plt.legend(loc='best') plt.xlabel('Time (sec)') plt.savefig('tclab_dyn_pred.png') plt.show() (:sourceend:) (:divend:)
Machine Learning Data and Solutions
<table> <tr> <td> <a target="_blank" href="https://www.amazon.com/gp/product/B07GMFWMRY/ref=as_li_tl?ie=UTF8&camp=1789&creative=9325&creativeASIN=B07GMFWMRY&linkCode=as2&tag=apmonitor-20&linkId=240e25095dffdf5a68ecc98a1b707e2f"><img border="0" src="//ws-na.amazon-adsystem.com/widgets/q?_encoding=UTF8&MarketPlace=US&ASIN=B07GMFWMRY&ServiceVersion=20070822&ID=AsinImage&WS=1&Format=_SL250_&tag=apmonitor-20" ></a><img src="//ir-na.amazon-adsystem.com/e/ir?t=apmonitor-20&l=am2&o=1&a=B07GMFWMRY" width="1" height="1" border="0" alt="" style="border:none !important; margin:0px !important;" /> </td> <td> <iframe style="width:120px;height:240px;" marginwidth="0" marginheight="0" scrolling="no" frameborder="0" src="//ws-na.amazon-adsystem.com/widgets/q?ServiceVersion=20070822&OneJS=1&Operation=GetAdHtml&MarketPlace=US&source=ac&ref=tf_til&ad_type=product_link&tracking_id=apmonitor-20&marketplace=amazon®ion=US&placement=B07GMFWMRY&asins=B07GMFWMRY&linkId=ef7e3c8c25c02a504ef84d62a51f77d9&show_border=false&link_opens_in_new_window=true&price_color=333333&title_color=0066c0&bg_color=ffffff"> </iframe> </td> </tr> </table> (:htmlend:)
(:html:)
<button class="button"><span>Purchase Lab Kit</span></button>
<button class="button"><span>Get Lab Kit</span></button>
(:toggle hide purchase button show="Get Temperature Control Lab":) (:div id=purchase:) The lab kit includes:
- Arduino Uno
- Temperature control PCB shield
- USB barrel jack power cable for heaters
- 5V USB power supply (US plug)
- USB cable for serial connection to MacOS, Windows, or Linux computer
- Small cardboard box
<form action="https://www.paypal.com/cgi-bin/webscr" method="post" target="_top"> <input type="hidden" name="cmd" value="_s-xclick"> <input type="hidden" name="hosted_button_id" value="CZWTTVAV9BJ8C"> <table> <tr><td><input type="hidden" name="on0" value="Lab Type">Lab Type</td></tr><tr><td><select name="os0">
<option value="Basic (PID) and Advanced Control (MPC) Kit">Basic (PID) and Advanced Control (MPC) Kit $35.00 USD</option>
</select> </td></tr> <tr><td><input type="hidden" name="on1" value="Firmware (can change later)">Arduino Firmware (can change later)</td></tr><tr><td><select name="os1">
<option value="MATLAB and Simulink">MATLAB and Simulink </option> <option value="Python">Python </option>
</select> </td></tr> <tr><td><input type="hidden" name="on2" value="Other notes (e.g. EU Plug)">Other notes (e.g. EU Plug)</td></tr><tr><td><input type="text" name="os2" maxlength="200"></td></tr> </table> <input type="hidden" name="currency_code" value="USD"> <input type="image" src="https://www.paypalobjects.com/en_US/i/btn/btn_buynowCC_LG.gif0" name="submit" alt="PayPal - The safer, easier way to pay online!"> <img alt="" border="0" src="https://www.paypalobjects.com/en_US/i/scr/pixel.gif1" height="1"> </form>
<a href='https://apmonitor.com/pdc/index.php/Main/PurchaseLabKit'> <button class="button"><span>Purchase Lab Kit</span></button> </a>
(:divend:)
(:htmlend:)
(:html:) <style> .button {
border-radius: 4px; background-color: #0000ff; border: none; color: #FFFFFF; text-align: center; font-size: 28px; padding: 20px; width: 200px; transition: all 0.5s; cursor: pointer; margin: 5px;
}
.button span {
cursor: pointer; display: inline-block; position: relative; transition: 0.5s;
}
.button span:after {
content: '\00bb'; position: absolute; opacity: 0; top: 0; right: -20px; transition: 0.5s;
}
.button:hover span {
padding-right: 25px;
}
.button:hover span:after {
opacity: 1; right: 0;
} </style>
(:html:) <script type="text/javascript"> _linkedin_partner_id = "452500"; window._linkedin_data_partner_ids = window._linkedin_data_partner_ids || []; window._linkedin_data_partner_ids.push(_linkedin_partner_id); </script><script type="text/javascript"> (function(){var s = document.getElementsByTagName("script")[0]; var b = document.createElement("script"); b.type = "text/javascript";b.async = true; b.src = "https://snap.licdn.com/li.lms-analytics/insight.min.js"; s.parentNode.insertBefore(b, s);})(); </script> <noscript> <img height="1" width="1" style="display:none;" alt="" src="https://dc.ads.linkedin.com/collect/?pid=452500&fmt=gif" /> </noscript> (:htmlend:)

(:html:) <table> <tr> <td> <a target="_blank" href="https://www.amazon.com/gp/product/B07GMFWMRY/ref=as_li_tl?ie=UTF8&camp=1789&creative=9325&creativeASIN=B07GMFWMRY&linkCode=as2&tag=apmonitor-20&linkId=240e25095dffdf5a68ecc98a1b707e2f"><img border="0" src="//ws-na.amazon-adsystem.com/widgets/q?_encoding=UTF8&MarketPlace=US&ASIN=B07GMFWMRY&ServiceVersion=20070822&ID=AsinImage&WS=1&Format=_SL250_&tag=apmonitor-20" ></a><img src="//ir-na.amazon-adsystem.com/e/ir?t=apmonitor-20&l=am2&o=1&a=B07GMFWMRY" width="1" height="1" border="0" alt="" style="border:none !important; margin:0px !important;" /> </td> <td> <iframe style="width:120px;height:240px;" marginwidth="0" marginheight="0" scrolling="no" frameborder="0" src="//ws-na.amazon-adsystem.com/widgets/q?ServiceVersion=20070822&OneJS=1&Operation=GetAdHtml&MarketPlace=US&source=ac&ref=tf_til&ad_type=product_link&tracking_id=apmonitor-20&marketplace=amazon®ion=US&placement=B07GMFWMRY&asins=B07GMFWMRY&linkId=ef7e3c8c25c02a504ef84d62a51f77d9&show_border=false&link_opens_in_new_window=true&price_color=333333&title_color=0066c0&bg_color=ffffff"> </iframe> </td> </tr> </table> (:htmlend:)
(:toggle init=hide id=mpc hide=mpc_siso_tclab.gif show=mpc_mimo_tclab.gif:)
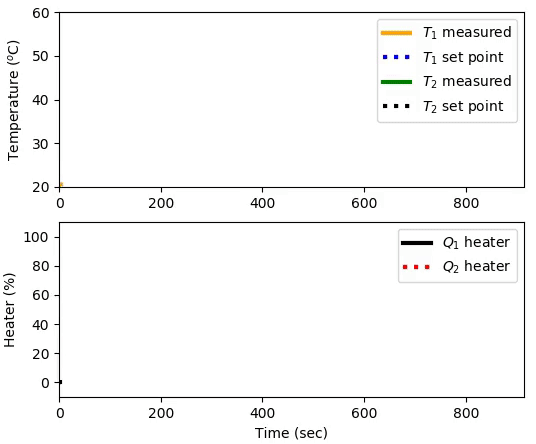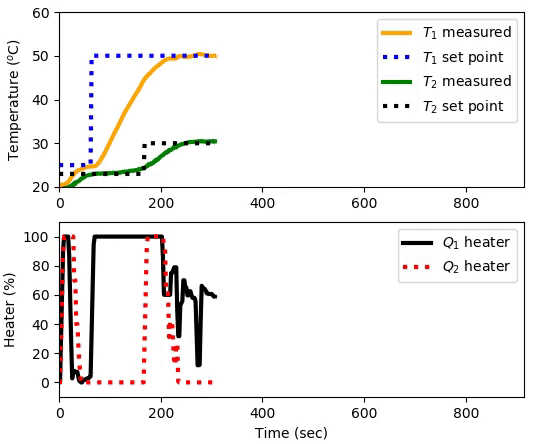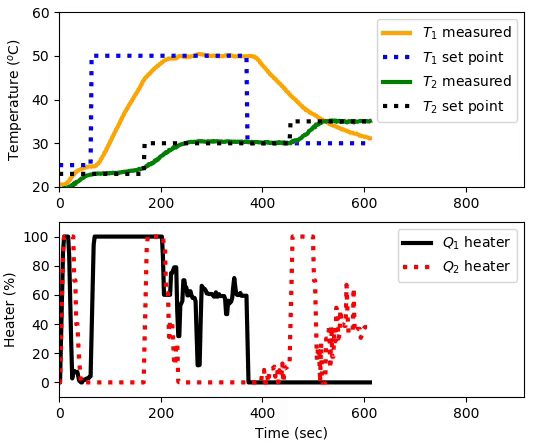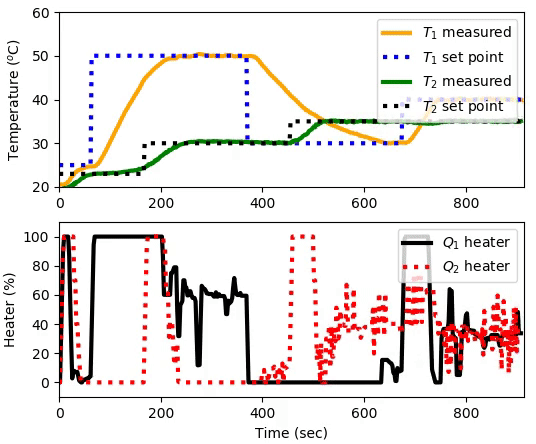
(:toggle init=hide id=mpc button=1 hide=mpc_siso_tclab.gif show=mpc_mimo_tclab.gif:)
(:toggle init=hide id=mpc hide=mpc_siso_tclab.gif show=mpc_mimo_tclab.gif:)
(:toggle init=hide button hide=mpc_siso_tclab.gif show=mpc_mimo_tclab.gif:)
(:toggle init=hide id=mpc button=1 hide=mpc_siso_tclab.gif show=mpc_mimo_tclab.gif:)
(:toggle init=hide hide=mpc_siso_tclab.gif show=mpc_mimo_tclab.gif:)
(:toggle init=hide button hide=mpc_siso_tclab.gif show=mpc_mimo_tclab.gif:)
(:toggle hide mimo button show="Show MIMO MPC":) (:div id=mimo:)

(:divend:)
(:toggle init=hide hide=mpc_siso_tclab.gif show=mpc_mimo_tclab.gif:)
(:toggle hide mimo button show="Show MIMO MPC":) (:div id=mimo:)

(:divend:)

These labs are hands-on applications of advanced temperature control with two heaters and two temperature sensors. The labs reinforce principles of model development, estimation, and advanced control methods.
This Arduino lab is a hands-on applications of advanced temperature control with two heaters and two temperature sensors. The labs reinforce principles of model development, estimation, and advanced control methods.
This lab is an application of advanced temperature control with two heaters and two temperature sensors.
These labs are hands-on applications of advanced temperature control with two heaters and two temperature sensors. The labs reinforce principles of model development, estimation, and advanced control methods.
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/dzl-h9_jP0o" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> (:htmlend:)
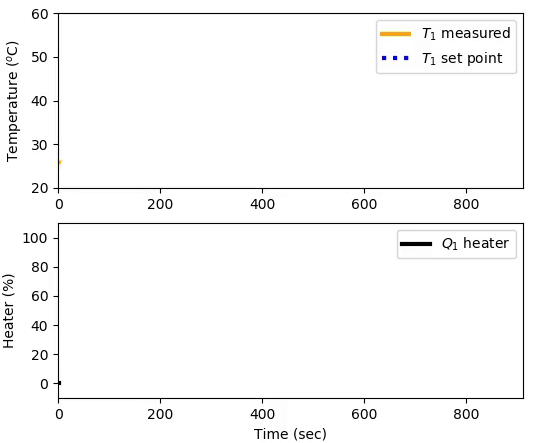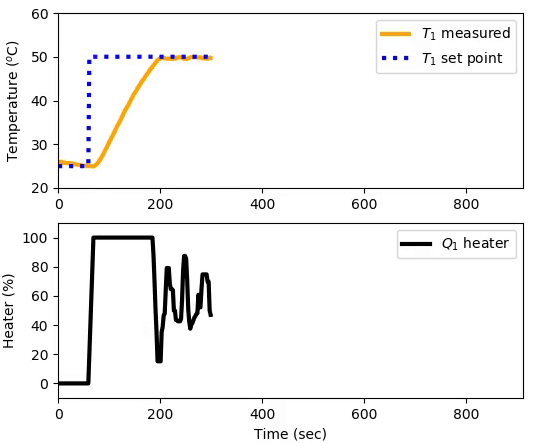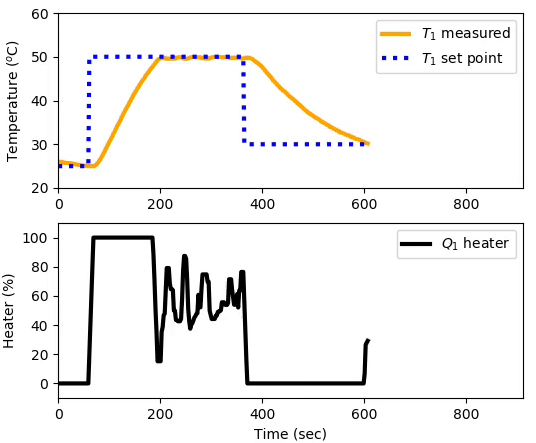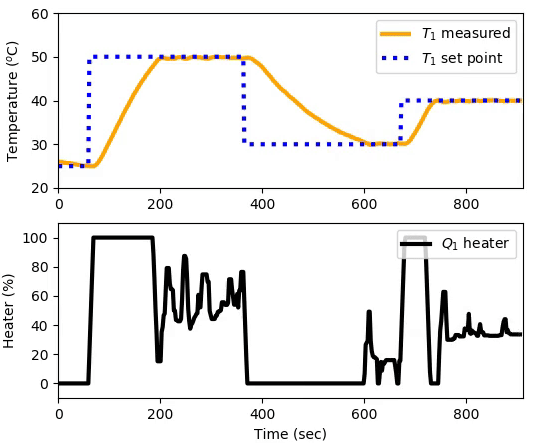
The heater power output is adjusted to maintain a desired temperature setpoint. Thermal energy from the heater is transferred by conduction, convection, and radiation to the temperature sensor.
The heater power output is adjusted to maintain a desired temperature setpoint. Thermal energy from the heater is transferred by conduction, convection, and radiation to the temperature sensor. This lab is a resource for model identification, estimation, and advanced control development.
This lab is a resource for model identification, estimation, and advanced control development with full source code examples available in MATLAB and Python.
- Lab F - Linear Model Predictive Control with Python and MATLAB Solutions
- Lab F - Linear Model Predictive Control with Python and MATLAB
- Lab F - Linear Model Predictive Control and Python (GEKKO) Solution and MATLAB Solution
- Lab F - Linear Model Predictive Control with Python and MATLAB Solutions
- Lab F - Linear Model Predictive Control and Solution
- Lab F - Linear Model Predictive Control and Python (GEKKO) Solution and MATLAB Solution
The advanced control lab explores multivariate control with Multiple Input Multiple Output (MIMO) modeling, estimation, and control.
This advanced control lab is for multivariate control with Multiple Input Multiple Output (MIMO) modeling, estimation, and control.
This lab is an application of advanced temperature control with two heaters and two temperature sensors. The heater power output is adjusted to maintain a desired temperature setpoint. Thermal energy from the heater is transferred by conduction, convection, and radiation to the temperature sensor. This lab is a resource for model identification, estimation, and advanced control development.
This lab is an application of advanced temperature control with two heaters and two temperature sensors.
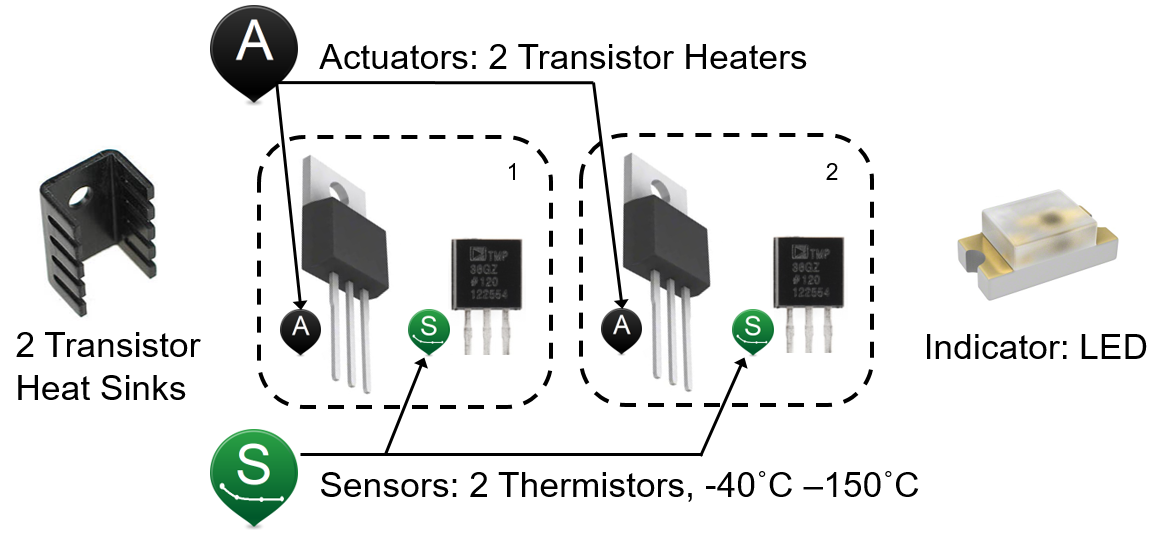
The heater power output is adjusted to maintain a desired temperature setpoint. Thermal energy from the heater is transferred by conduction, convection, and radiation to the temperature sensor. This lab is a resource for model identification, estimation, and advanced control development.

- and Solution
- and Solution
- Lab A - Single Heater Modeling and Solution
- Lab B - Dual Heater Modeling and Solution
- and Solution
- and Solution
- Lab C - Parameter Estimation and Solution
- Lab D - Empirical Model Estimation and Solution
- and Solution
- and Solution
- and Solution
- and Solution
- and Solution
- and Solution
- and Solution
- and Solution
(:title Advanced Temperature Control:) (:keywords Arduino, PID, temperature, control, process control, course:) (:description Temperature Control with an Arduino Device:)
This lab is an application of advanced temperature control with two heaters and two temperature sensors. The heater power output is adjusted to maintain a desired temperature setpoint. Thermal energy from the heater is transferred by conduction, convection, and radiation to the temperature sensor. This lab is a resource for model identification, estimation, and advanced control development.

(:toggle hide purchase button show="Get Temperature Control Lab":) (:div id=purchase:) The lab kit includes:
- Arduino Uno
- Temperature control PCB shield
- USB barrel jack power cable for heaters
- 5V USB power supply (US plug)
- USB cable for serial connection to MacOS, Windows, or Linux computer
- Small cardboard box

(:html:) <form action="https://www.paypal.com/cgi-bin/webscr" method="post" target="_top"> <input type="hidden" name="cmd" value="_s-xclick"> <input type="hidden" name="hosted_button_id" value="CZWTTVAV9BJ8C"> <table> <tr><td><input type="hidden" name="on0" value="Lab Type">Lab Type</td></tr><tr><td><select name="os0">
<option value="Basic (PID) and Advanced Control (MPC) Kit">Basic (PID) and Advanced Control (MPC) Kit $35.00 USD</option>
</select> </td></tr> <tr><td><input type="hidden" name="on1" value="Firmware (can change later)">Arduino Firmware (can change later)</td></tr><tr><td><select name="os1">
<option value="MATLAB and Simulink">MATLAB and Simulink </option> <option value="Python">Python </option>
</select> </td></tr> <tr><td><input type="hidden" name="on2" value="Other notes (e.g. EU Plug)">Other notes (e.g. EU Plug)</td></tr><tr><td><input type="text" name="os2" maxlength="200"></td></tr> </table> <input type="hidden" name="currency_code" value="USD"> <input type="image" src="https://www.paypalobjects.com/en_US/i/btn/btn_buynowCC_LG.gif0" name="submit" alt="PayPal - The safer, easier way to pay online!"> <img alt="" border="0" src="https://www.paypalobjects.com/en_US/i/scr/pixel.gif1" height="1"> </form> (:htmlend:) (:divend:)

Lab Resources
Lab software is available in MATLAB, Python, and Simulink. The GEKKO package is recommended for Python or first-time users without a language preference.
- TCLab Files on GitHub
A basic version of this lab is also available. The more basic lab instructions are for tuning a Proportional Integral Derivative (PID) controller with Single Input Single Output (SISO) control.
- Basic (PID) Control Lab
The advanced control lab explores multivariate control with Multiple Input Multiple Output (MIMO) modeling, estimation, and control.
Lab Instructions
The advanced control lab has three phases including model development, parameter and state estimation, and advanced control. The models developed and tuned in the initial phase are used directly in model predictive control. Model forms are from empirical identification or fundamental energy balance relationships and include single (SISO) and dual heater (MIMO) modules. Relationships may be linear or nonlinear with continuous or discrete variables.
Model Development
- and Solution
- and Solution
Parameter and State Estimation
- and Solution
- and Solution